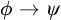1 results
CRAIG INTERPOLATION THEOREM FAILS IN BI-INTUITIONISTIC PREDICATE LOGIC
- Part of
-
- Journal:
- The Review of Symbolic Logic / Volume 17 / Issue 2 / June 2024
- Published online by Cambridge University Press:
- 12 August 2022, pp. 611-633
- Print publication:
- June 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
-
In this article we show that bi-intuitionistic predicate logic lacks the Craig Interpolation Property. We proceed by adapting the counterexample given by Mints, Olkhovikov and Urquhart for intuitionistic predicate logic with constant domains [13]. More precisely, we show that there is a valid implication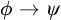
$\phi \rightarrow \psi $ with no interpolant. Importantly, this result does not contradict the unfortunately named ‘Craig interpolation’ theorem established by Rauszer in [24] since that article is about the property more correctly named ‘deductive interpolation’ (see Galatos, Jipsen, Kowalski and Ono’s use of this term in [5]) for global consequence. Given that the deduction theorem fails for bi-intuitionistic logic with global consequence, the two formulations of the property are not equivalent.
