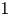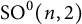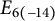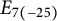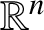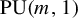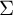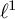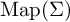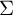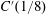9 results
Volume and Euler classes in bounded cohomology of transformation groups
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 67 / Issue 1 / January 2025
- Published online by Cambridge University Press:
- 02 October 2024, pp. 34-49
- Print publication:
- January 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
On stable commutator length of non-filling curves in surfaces
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 14 December 2023, pp. 1-18
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Bounded cohomology is not a profinite invariant
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 67 / Issue 2 / June 2024
- Published online by Cambridge University Press:
- 20 October 2023, pp. 379-390
- Print publication:
- June 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
BOUNDED COHOMOLOGY AND BINATE GROUPS
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 115 / Issue 2 / October 2023
- Published online by Cambridge University Press:
- 10 May 2022, pp. 204-239
- Print publication:
- October 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Multiplicative constants and maximal measurable cocycles in bounded cohomology
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 42 / Issue 11 / November 2022
- Published online by Cambridge University Press:
- 31 August 2021, pp. 3490-3525
- Print publication:
- November 2022
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
BIG MAPPING CLASS GROUPS WITH HYPERBOLIC ACTIONS: CLASSIFICATION AND APPLICATIONS
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 21 / Issue 6 / November 2022
- Published online by Cambridge University Press:
- 31 May 2021, pp. 2173-2204
- Print publication:
- November 2022
-
- Article
- Export citation
Geometry of Infinitely Presented Small Cancellation Groups and Quasi-homomorphisms
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 71 / Issue 5 / October 2019
- Published online by Cambridge University Press:
- 09 January 2019, pp. 997-1018
- Print publication:
- October 2019
-
- Article
-
- You have access
- Export citation
Simplicial cohomology of augmentation ideals in l1(G)
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 53 / Issue 1 / February 2010
- Published online by Cambridge University Press:
- 12 January 2010, pp. 97-109
-
- Article
-
- You have access
- Export citation
The second bounded cohomology of a group acting on a Gromov-hyperbolic space
-
- Journal:
- Proceedings of the London Mathematical Society / Volume 76 / Issue 1 / January 1998
- Published online by Cambridge University Press:
- 01 January 1998, pp. 70-94
- Print publication:
- January 1998
-
- Article
- Export citation