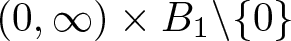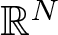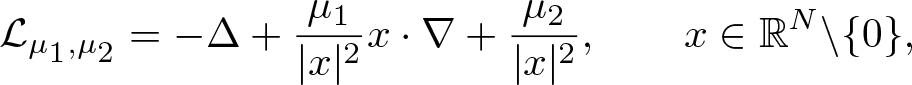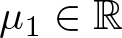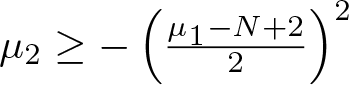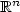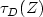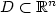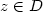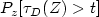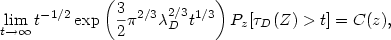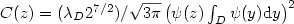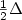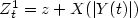2 results
Higher-order evolution inequalities involving convection and Hardy-Leray potential terms in a bounded domain
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 66 / Issue 2 / May 2023
- Published online by Cambridge University Press:
- 05 May 2023, pp. 366-390
-
- Article
- Export citation
Lifetime asymptotics of iterated Brownian motion in $\mathbb{R}^{n}$
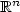
-
- Journal:
- ESAIM: Probability and Statistics / Volume 11 / June 2007
- Published online by Cambridge University Press:
- 31 March 2007, pp. 147-160
- Print publication:
- June 2007
-
- Article
- Export citation