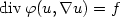We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
We present the numerical analysis on the Poisson problem of two mixed Petrov-Galerkin finite volume schemes for equations in divergence form $\mathop{\rm div}\nolimits\varphi(u,\nabla u)=f$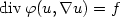 
. The first scheme, which has been introduced in [CITE], is a generalization in two dimensions of Keller's box-scheme. The second scheme is the dual of the first one, and is a cell-centeredscheme for u and the flux φ. For the first scheme, the two trial finite element spaces are the nonconforming space of Crouzeix-Raviartfor the primal unknown u and the div-conformingspace of Raviart-Thomas for the flux φ. The two test spaces are the functions constant per cell both for the conservative and for the fluxequations.We prove an optimal second order error estimate for the box scheme and we emphasize the link between this scheme and the post-processing of Arnold and Brezzi of the classical mixed method.
