1 results
On the derived category of the Iwahori–Hecke algebra
- Part of
-
- Journal:
- Compositio Mathematica / Volume 159 / Issue 5 / May 2023
- Published online by Cambridge University Press:
- 04 May 2023, pp. 1042-1110
- Print publication:
- May 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
-
We state a conjecture that relates the derived category of smooth representations of a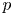
$p$-adic split reductive group with the derived category of (quasi-)coherent sheaves on a stack of L-parameters. We investigate the conjecture in the case of the principal block of 
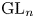${\rm GL}_n$ by showing that the functor should be given by the derived tensor product with the family of representations interpolating the modified Langlands correspondence over the stack of L-parameters that is suggested by the work of Helm and of Emerton and Helm.
