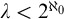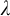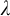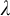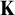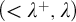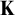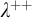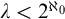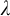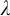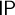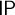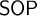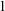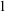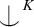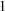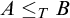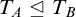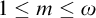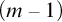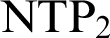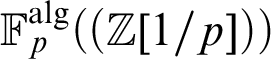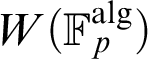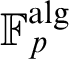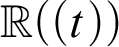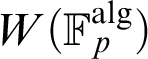In this thesis, we study transfer principles in the context of certain Henselian valued fields, namely Henselian valued fields of equicharacteristic  0
, algebraically closed valued fields, algebraically maximal Kaplansky valued fields, and unramified mixed characteristic Henselian valued fields with perfect residue field. First, we compute the burden of such a valued field in terms of the burden of its value group and its residue field. The burden is a cardinal related to the model theoretic complexity and a notion of dimension associated to
0
, algebraically closed valued fields, algebraically maximal Kaplansky valued fields, and unramified mixed characteristic Henselian valued fields with perfect residue field. First, we compute the burden of such a valued field in terms of the burden of its value group and its residue field. The burden is a cardinal related to the model theoretic complexity and a notion of dimension associated to 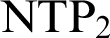 \text {NTP}_2
theories. We show, for instance, that the Hahn field
\text {NTP}_2
theories. We show, for instance, that the Hahn field 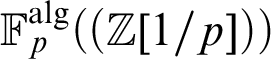 \mathbb {F}_p^{\text {alg}}((\mathbb {Z}[1/p]))
is inp-minimal (of burden 1), and that the ring of Witt vectors
\mathbb {F}_p^{\text {alg}}((\mathbb {Z}[1/p]))
is inp-minimal (of burden 1), and that the ring of Witt vectors 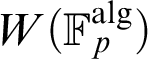 W(\mathbb {F}_p^{\text {alg}})
over
W(\mathbb {F}_p^{\text {alg}})
over 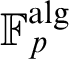 \mathbb {F}_p^{\text {alg}}
is not strong (of burden
\mathbb {F}_p^{\text {alg}}
is not strong (of burden  \omega
). This result extends previous work by Chernikov and Simon and realizes an important step toward the classification of Henselian valued fields of finite burden. Second, we show a transfer principle for the property that all types realized in a given elementary extension are definable. It can be written as follows: a valued field as above is stably embedded in an elementary extension if and only if its value group is stably embedded in the corresponding extension of value groups, its residue field is stably embedded in the corresponding extension of residue fields, and the extension of valued fields satisfies a certain algebraic condition. We show, for instance, that all types over the power series field
\omega
). This result extends previous work by Chernikov and Simon and realizes an important step toward the classification of Henselian valued fields of finite burden. Second, we show a transfer principle for the property that all types realized in a given elementary extension are definable. It can be written as follows: a valued field as above is stably embedded in an elementary extension if and only if its value group is stably embedded in the corresponding extension of value groups, its residue field is stably embedded in the corresponding extension of residue fields, and the extension of valued fields satisfies a certain algebraic condition. We show, for instance, that all types over the power series field 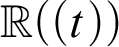 \mathbb {R}((t))
are definable. Similarly, all types over the quotient field of
\mathbb {R}((t))
are definable. Similarly, all types over the quotient field of 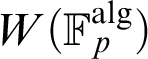 W(\mathbb {F}_p^{\text {alg}})
are definable. This extends previous work of Cubides and Delon and of Cubides and Ye.
W(\mathbb {F}_p^{\text {alg}})
are definable. This extends previous work of Cubides and Delon and of Cubides and Ye.
These distinct results use a common approach, which has been developed recently. It consists of establishing first a reduction to an intermediate structure called the leading term structure, or  \operatorname {\mathrm {RV}}
-sort, and then of reducing to the value group and residue field. This leads us to develop similar reduction principles in the context of pure short exact sequences of abelian groups.
\operatorname {\mathrm {RV}}
-sort, and then of reducing to the value group and residue field. This leads us to develop similar reduction principles in the context of pure short exact sequences of abelian groups.
Abstract prepared by Pierre Touchard.
E-mail: pierre.pa.touchard@gmail.com
URL: https://miami.uni-muenster.de/Record/a612cf73-0a2f-42c4-b1e4-7d28934138a9