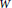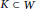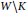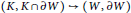11 results
A Remark on Configuration Spaces of Two Points
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 61 / Issue 2 / May 2018
- Published online by Cambridge University Press:
- 11 April 2018, pp. 599-605
-
- Article
- Export citation
Rational Models of the Complement of a Subpolyhedron in a Manifold with Boundary
-
- Journal:
- Canadian Journal of Mathematics / Volume 70 / Issue 2 / 01 April 2018
- Published online by Cambridge University Press:
- 20 November 2018, pp. 265-293
- Print publication:
- 01 April 2018
-
- Article
-
- You have access
- Export citation
TELESCOPIC LINKAGES AND A TOPOLOGICAL APPROACH TO PHASE TRANSITIONS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 90 / Issue 2 / April 2011
- Published online by Cambridge University Press:
- 03 June 2011, pp. 183-195
- Print publication:
- April 2011
-
- Article
-
- You have access
- Export citation