1 results
The topology of compact rank-one ECS manifolds
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 66 / Issue 3 / August 2023
- Published online by Cambridge University Press:
- 17 August 2023, pp. 789-809
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
-
Pseudo-Riemannian manifolds with parallel Weyl tensor that are not conformally flat or locally symmetric, also known as essentially conformally symmetric (ECS) manifolds, have a natural local invariant, the rank, which equals 1 or 2, and is the rank of a certain distinguished null parallel distribution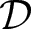
$\mathcal{D}$. All known examples of compact ECS manifolds are of rank one and have dimensions greater than 4. We prove that a compact rank-one ECS manifold, if not locally homogeneous, replaced when necessary by a twofold isometric covering, must be a bundle over the circle with leaves of 
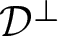$\mathcal{D}^\perp$ serving as the fibres. The same conclusion holds in the locally homogeneous case if one assumes that 
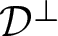$\,\mathcal{D}^\perp$ has at least one compact leaf. We also show that in the pseudo-Riemannian universal covering space of any compact rank-one ECS manifold, the leaves of 
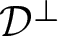$\mathcal{D}^\perp$ are the factor manifolds of a global product decomposition.
