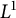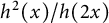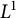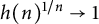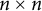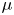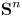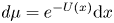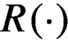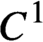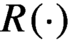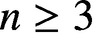Refine search
Actions for selected content:
59 results
3 - Optimization Theory and Algorithms
-
- Book:
- Mathematical Methods in Data Science
- Published online:
- 04 November 2025
- Print publication:
- 30 October 2025, pp 128-199
-
- Chapter
- Export citation
10 - Quantification of Quantum Resources
- from Part III - The General Framework of Resource Theories
-
- Book:
- Quantum Resource Theories
- Published online:
- 03 May 2025
- Print publication:
- 10 April 2025, pp 426-466
-
- Chapter
- Export citation
Appendix B - Elements of Convex Analysis
-
- Book:
- Theoretical Foundations of Asset Pricing
- Published online:
- 06 February 2025
- Print publication:
- 13 February 2025, pp 206-231
-
- Chapter
- Export citation
14 - Vectors, Preferences and Convexity
-
- Book:
- Mathematics for Economics and Finance
- Published online:
- 24 May 2024
- Print publication:
- 30 May 2024, pp 137-151
-
- Chapter
- Export citation
On some convexity questions of Handelman
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 67 / Issue 4 / December 2024
- Published online by Cambridge University Press:
- 16 May 2024, pp. 936-939
- Print publication:
- December 2024
-
- Article
- Export citation
Multidimensional random motions with a natural number of finite velocities
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 56 / Issue 3 / September 2024
- Published online by Cambridge University Press:
- 22 March 2024, pp. 1033-1063
- Print publication:
- September 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
ON SEPARATE CONTINUITY AND SEPARATE CONVEXITY: A SYNTHETIC TREATMENT FOR FUNCTIONS AND SETS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 109 / Issue 3 / June 2024
- Published online by Cambridge University Press:
- 17 July 2023, pp. 541-551
- Print publication:
- June 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Norms on complex matrices induced by random vectors
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 66 / Issue 3 / September 2023
- Published online by Cambridge University Press:
- 23 December 2022, pp. 808-826
- Print publication:
- September 2023
-
- Article
- Export citation
6 - There Is No Thermodynamic Arrow
-
- Book:
- Reversing the Arrow of Time
- Published online:
- 24 November 2022
- Print publication:
- 08 December 2022, pp 139-167
-
- Chapter
-
- You have access
- Open access
- Export citation
Appendix B - Basic Analysis Review
-
- Book:
- Classical Numerical Analysis
- Published online:
- 29 September 2022
- Print publication:
- 20 October 2022, pp 854-873
-
- Chapter
- Export citation
16 - Convex Optimization
- from Part III - Nonlinear Equations and Optimization
-
- Book:
- Classical Numerical Analysis
- Published online:
- 29 September 2022
- Print publication:
- 20 October 2022, pp 451-506
-
- Chapter
- Export citation
Transportation on spheres via an entropy formula
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 153 / Issue 5 / October 2023
- Published online by Cambridge University Press:
- 05 September 2022, pp. 1467-1478
- Print publication:
- October 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
THE SECOND SHIFTED DIFFERENCE OF PARTITIONS AND ITS APPLICATIONS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 107 / Issue 1 / February 2023
- Published online by Cambridge University Press:
- 25 August 2022, pp. 66-78
- Print publication:
- February 2023
-
- Article
- Export citation
On equal-input and monotone Markov matrices
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 54 / Issue 2 / June 2022
- Published online by Cambridge University Press:
- 06 June 2022, pp. 460-492
- Print publication:
- June 2022
-
- Article
- Export citation
11 - Interest Rate Risk
-
- Book:
- Quantitative Enterprise Risk Management
- Published online:
- 28 July 2022
- Print publication:
- 05 May 2022, pp 307-335
-
- Chapter
- Export citation
2 - Foundations of Smooth Optimization
-
- Book:
- Optimization for Data Analysis
- Published online:
- 31 March 2022
- Print publication:
- 21 April 2022, pp 15-25
-
- Chapter
- Export citation
3 - Basic Theoretical Concepts in Optimization
-
- Book:
- Advanced Optimization for Process Systems Engineering
- Published online:
- 11 June 2021
- Print publication:
- 25 March 2021, pp 16-31
-
- Chapter
- Export citation
4 - Quadratic Functions
- from Part II - From General Mathematical Background to General Nonlinear Programming Problems (NLP)
-
- Book:
- Optimization for Chemical and Biochemical Engineering
- Published online:
- 17 December 2020
- Print publication:
- 14 January 2021, pp 44-56
-
- Chapter
- Export citation
Generic rotation sets
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 42 / Issue 1 / January 2022
- Published online by Cambridge University Press:
- 29 December 2020, pp. 250-262
- Print publication:
- January 2022
-
- Article
- Export citation
STARLIKENESS AND CONVEXITY OF CAUCHY TRANSFORMS ON REGULAR POLYGONS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 103 / Issue 2 / April 2021
- Published online by Cambridge University Press:
- 05 October 2020, pp. 291-302
- Print publication:
- April 2021
-
- Article
- Export citation