We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
We advance a new conjecture in the spirit of the dynamical Manin–Mumford conjecture. We show that our conjecture holds for all polarisable endomorphisms of abelian varieties and for all polarisable endomorphisms of 
$(\mathbb{P}^{1})^{N}$. Furthermore, we show various examples which highlight the restrictions one would need to consider in formulating any general conclusion in the dynamical Manin–Mumford conjecture.
$(\mathbb{P}^{1})^{n}$
We prove Zhang’s dynamical Manin–Mumford conjecture and dynamical Bogomolov conjecture for dominant endomorphisms
$\unicode[STIX]{x1D6F7}$
of
$(\mathbb{P}^{1})^{n}$
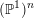. We use the equidistribution theorem for points of small height with respect to an algebraic dynamical system, combined with an analysis of the symmetries of the Julia set for a rational function.
