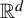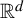1 results
On arithmetic progressions in non-periodic self-affine tilings
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 42 / Issue 9 / September 2022
- Published online by Cambridge University Press:
- 15 June 2021, pp. 2957-2989
- Print publication:
- September 2022
-
- Article
- Export citation
-
We study the repetition of patches in self-affine tilings in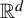
${\mathbb {R}}^d$
. In particular, we study the existence and non-existence of arithmetic progressions. We first show that an arithmetic condition of the expansion map for a self-affine tiling implies the non-existence of certain one-dimensional arithmetic progressions. Next, we show that the existence of full-rank infinite arithmetic progressions, pure discrete dynamical spectrum, and limit-periodicity are all equivalent for a certain class of self-affine tilings. We finish by giving a complete picture for the existence or non-existence of full-rank infinite arithmetic progressions in the self-similar tilings in 
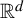${\mathbb {R}}^d$
.
