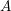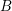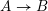3 results
WHEN IS A NUMERICAL SEMIGROUP A QUOTIENT?
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 109 / Issue 1 / February 2024
- Published online by Cambridge University Press:
- 10 February 2023, pp. 67-76
- Print publication:
- February 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
HRV analysis: undependability of approximate entropy at locating optimum complexity in malnourished children
- Part of
-
- Journal:
- Cardiology in the Young / Volume 32 / Issue 3 / March 2022
- Published online by Cambridge University Press:
- 17 June 2021, pp. 425-430
-
- Article
- Export citation
Proof of de Smit’s conjecture: a freeness criterion
- Part of
-
- Journal:
- Compositio Mathematica / Volume 153 / Issue 11 / November 2017
- Published online by Cambridge University Press:
- 14 August 2017, pp. 2310-2317
- Print publication:
- November 2017
-
- Article
- Export citation