Let (X, cX) be a convex projective surface equipped with a real structure. The space of stable maps 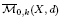 carries different real structures induced by cX and any order two element τ of permutation group Sk acting on marked points. Each corresponding real part ℝτ
carries different real structures induced by cX and any order two element τ of permutation group Sk acting on marked points. Each corresponding real part ℝτ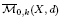 is a real normal projective variety. As the singular locus is of codimension bigger than two, these spaces thus carry a first Stiefel–Whitney class for which we determine a representative in the case k = c1(X)d − 1 where c1(X) is the first Chern class of X. Namely, we give a homological description of these classes in term of the real part of boundary divisors of the space of stable maps.
is a real normal projective variety. As the singular locus is of codimension bigger than two, these spaces thus carry a first Stiefel–Whitney class for which we determine a representative in the case k = c1(X)d − 1 where c1(X) is the first Chern class of X. Namely, we give a homological description of these classes in term of the real part of boundary divisors of the space of stable maps.