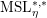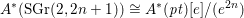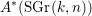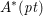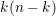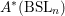8 results
Volume and Euler classes in bounded cohomology of transformation groups
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 67 / Issue 1 / January 2025
- Published online by Cambridge University Press:
- 02 October 2024, pp. 34-49
- Print publication:
- January 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
EULER CLASSES: SIX-FUNCTORS FORMALISM, DUALITIES, INTEGRALITY AND LINEAR SUBSPACES OF COMPLETE INTERSECTIONS
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 22 / Issue 2 / March 2023
- Published online by Cambridge University Press:
- 16 July 2021, pp. 681-746
- Print publication:
- March 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
An arithmetic count of the lines on a smooth cubic surface
- Part of
-
- Journal:
- Compositio Mathematica / Volume 157 / Issue 4 / April 2021
- Published online by Cambridge University Press:
- 08 April 2021, pp. 677-709
- Print publication:
- April 2021
-
- Article
- Export citation
On Homotopy Invariants of Combings of Three-manifolds
-
- Journal:
- Canadian Journal of Mathematics / Volume 67 / Issue 1 / 01 February 2015
- Published online by Cambridge University Press:
- 20 November 2018, pp. 152-183
- Print publication:
- 01 February 2015
-
- Article
-
- You have access
- Export citation
The special linear version of the projective bundle theorem
- Part of
-
- Journal:
- Compositio Mathematica / Volume 151 / Issue 3 / March 2015
- Published online by Cambridge University Press:
- 07 November 2014, pp. 461-501
- Print publication:
- March 2015
-
- Article
- Export citation
From Symmetries of the Modular Tower of Genus Zero Real Stable Curves to a Euler Class for the Dyadic Circle
-
- Journal:
- Compositio Mathematica / Volume 137 / Issue 1 / May 2003
- Published online by Cambridge University Press:
- 04 December 2007, pp. 49-73
- Print publication:
- May 2003
-
- Article
-
- You have access
- Export citation
EQUIVARIANT FORMAL GROUP LAWS
-
- Journal:
- Proceedings of the London Mathematical Society / Volume 81 / Issue 2 / September 2000
- Published online by Cambridge University Press:
- 19 October 2000, pp. 355-386
- Print publication:
- September 2000
-
- Article
- Export citation
Free Group Actions on Spaces Homotopy Equivalent to a Sphere
-
- Journal:
- Compositio Mathematica / Volume 120 / Issue 3 / February 2000
- Published online by Cambridge University Press:
- 04 December 2007, pp. 327-333
- Print publication:
- February 2000
-
- Article
-
- You have access
- Export citation