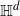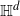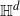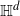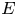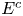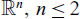14 results
8 - Non-Hermitian Quantum Physics
-
- Book:
- A Computational Introduction to Quantum Physics
- Published online:
- 24 April 2024
- Print publication:
- 25 April 2024, pp 152-164
-
- Chapter
- Export citation
Thin-ended clusters in percolation in
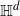 $\mathbb{H}^d$
$\mathbb{H}^d$
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 55 / Issue 2 / June 2023
- Published online by Cambridge University Press:
- 10 March 2023, pp. 581-610
- Print publication:
- June 2023
-
- Article
- Export citation
Exponential decay for the KdV equation on ℝ with new localized dampings
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 153 / Issue 4 / August 2023
- Published online by Cambridge University Press:
- 05 April 2022, pp. 1073-1098
- Print publication:
- August 2023
-
- Article
- Export citation
Global and exponential attractor of the repulsive Keller–Segel model with logarithmic sensitivity
- Part of
-
- Journal:
- European Journal of Applied Mathematics / Volume 32 / Issue 4 / August 2021
- Published online by Cambridge University Press:
- 30 June 2020, pp. 599-617
-
- Article
- Export citation
Samples with a limit shape, multivariate extremes, and risk
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 52 / Issue 2 / June 2020
- Published online by Cambridge University Press:
- 15 July 2020, pp. 491-522
- Print publication:
- June 2020
-
- Article
- Export citation
15 - Exponential Decay
- from Part III - The Banach Space Setting
-
- Book:
- Operator-Adapted Wavelets, Fast Solvers, and Numerical Homogenization
- Published online:
- 10 October 2019
- Print publication:
- 24 October 2019, pp 252-296
-
- Chapter
- Export citation
Some sharp results about the global existence and blowup of solutions to a class of pseudo-parabolic equations
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 147 / Issue 6 / December 2017
- Published online by Cambridge University Press:
- 14 August 2017, pp. 1311-1331
- Print publication:
- December 2017
-
- Article
- Export citation
Fast Solution of Three-Dimensional Modified Helmholtz Equations by the Method of Fundamental Solutions
- Part of
-
- Journal:
- Communications in Computational Physics / Volume 20 / Issue 2 / August 2016
- Published online by Cambridge University Press:
- 21 July 2016, pp. 512-533
- Print publication:
- August 2016
-
- Article
- Export citation
Stabilization of Regular Solutions for the Zakharov-Kuznetsov Equation Posed on Bounded Rectangles and on a Strip
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 58 / Issue 3 / October 2015
- Published online by Cambridge University Press:
- 10 April 2015, pp. 661-682
-
- Article
- Export citation
Representations for the Decay Parameter of a Birth-Death Process Based on the Courant-Fischer Theorem
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 52 / Issue 1 / March 2015
- Published online by Cambridge University Press:
- 30 January 2018, pp. 278-289
- Print publication:
- March 2015
-
- Article
-
- You have access
- Export citation
A Variability Study of Long-term Optical Data of OJ 287
-
- Journal:
- Proceedings of the International Astronomical Union / Volume 8 / Issue S290 / August 2012
- Published online by Cambridge University Press:
- 21 February 2013, pp. 269-270
- Print publication:
- August 2012
-
- Article
-
- You have access
- Export citation
A Carleman estimates based approach for the stabilization of some locally damped semilinear hyperbolic equations
-
- Journal:
- ESAIM: Control, Optimisation and Calculus of Variations / Volume 14 / Issue 3 / July 2008
- Published online by Cambridge University Press:
- 21 December 2007, pp. 561-574
- Print publication:
- July 2008
-
- Article
- Export citation
attention-deficit/hyperactivity disorder (adhd): delay-of-reinforcement gradients and other behavioral mechanisms
-
- Journal:
- Behavioral and Brain Sciences / Volume 28 / Issue 3 / June 2005
- Published online by Cambridge University Press:
- 07 September 2005, pp. 419-424
-
- Article
- Export citation
Large deviations and the Bayesian estimation of higher-order Markov transition functions
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 33 / Issue 1 / March 1996
- Published online by Cambridge University Press:
- 14 July 2016, pp. 18-27
- Print publication:
- March 1996
-
- Article
- Export citation