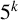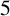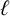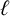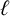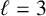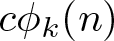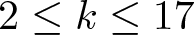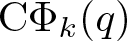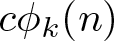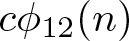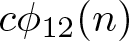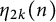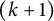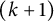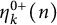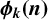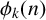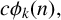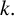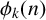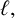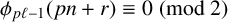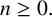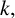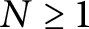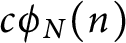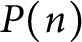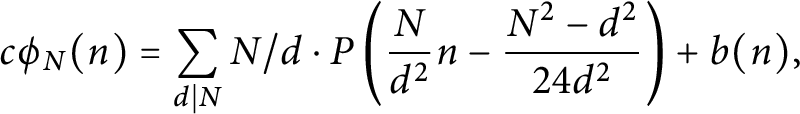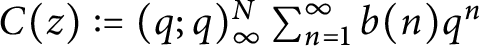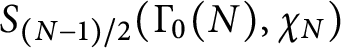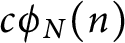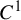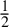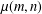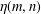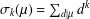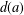Refine search
Actions for selected content:
54 results
Temporal configuration model: Statistical inference and spreading processes
-
- Journal:
- Network Science / Volume 13 / 2025
- Published online by Cambridge University Press:
- 11 December 2025, e22
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
8 - Generating Functions and Chain Reactions
-
- Book:
- Probability Theory for Quantitative Scientists
- Published online:
- 24 July 2025
- Print publication:
- 14 August 2025, pp 217-229
-
- Chapter
- Export citation
ON
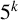 $5^k$-REGULAR PARTITIONS MODULO POWERS OF
$5^k$-REGULAR PARTITIONS MODULO POWERS OF 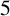 $5$
$5$
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 112 / Issue 3 / December 2025
- Published online by Cambridge University Press:
- 14 April 2025, pp. 449-457
- Print publication:
- December 2025
-
- Article
- Export citation
EXTENDING CONGRUENCES FOR OVERPARTITIONS WITH
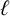 $\ell $-REGULAR NONOVERLINED PARTS
$\ell $-REGULAR NONOVERLINED PARTS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 111 / Issue 3 / June 2025
- Published online by Cambridge University Press:
- 25 November 2024, pp. 478-489
- Print publication:
- June 2025
-
- Article
- Export citation
Chapter 22 - Network models
- from Part III - Fundamentals
-
- Book:
- Working with Network Data
- Published online:
- 06 June 2024
- Print publication:
- 13 June 2024, pp 327-350
-
- Chapter
- Export citation
Some congruences for 12-coloured generalized Frobenius partitions
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 67 / Issue 3 / August 2024
- Published online by Cambridge University Press:
- 02 May 2024, pp. 778-793
-
- Article
- Export citation
The distribution of the maximum protection number in simply generated trees
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 33 / Issue 4 / July 2024
- Published online by Cambridge University Press:
- 12 April 2024, pp. 518-553
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Burstein’s permutation conjecture, Hong and Li’s inversion sequence conjecture and restricted Eulerian distributions
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 66 / Issue 4 / November 2023
- Published online by Cambridge University Press:
- 23 October 2023, pp. 1179-1201
-
- Article
- Export citation
Asymptotics for symmetrized positive moments of odd ranks
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 76 / Issue 5 / October 2024
- Published online by Cambridge University Press:
- 09 October 2023, pp. 1731-1752
- Print publication:
- October 2024
-
- Article
- Export citation
2 - The Conway–Maxwell–Poisson (COM–Poisson) Distribution
-
- Book:
- The Conway–Maxwell–Poisson Distribution
- Published online:
- 02 March 2023
- Print publication:
- 09 March 2023, pp 22-70
-
- Chapter
- Export citation
Sturm–Liouville theory and decay parameter for quadratic markov branching processes
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 60 / Issue 3 / September 2023
- Published online by Cambridge University Press:
- 19 January 2023, pp. 737-764
- Print publication:
- September 2023
-
- Article
- Export citation
On the Hofer–Zehnder conjecture on weighted projective spaces
- Part of
-
- Journal:
- Compositio Mathematica / Volume 159 / Issue 1 / January 2023
- Published online by Cambridge University Press:
- 23 January 2023, pp. 87-108
- Print publication:
- January 2023
-
- Article
- Export citation
ON THE PARITY OF THE GENERALISED FROBENIUS PARTITION FUNCTIONS
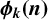 $\boldsymbol {\phi _k(n)}$
$\boldsymbol {\phi _k(n)}$
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 106 / Issue 3 / December 2022
- Published online by Cambridge University Press:
- 15 June 2022, pp. 431-436
- Print publication:
- December 2022
-
- Article
- Export citation
Some cases of Kudla’s modularity conjecture for unitary Shimura varieties
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 10 / 2022
- Published online by Cambridge University Press:
- 09 June 2022, e37
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
N-colored generalized Frobenius partitions: generalized Kolitsch identities
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 75 / Issue 2 / April 2023
- Published online by Cambridge University Press:
- 25 January 2022, pp. 447-469
- Print publication:
- April 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Actions of symplectic homeomorphisms/diffeomorphisms on foliations by curves in dimension 2
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 43 / Issue 3 / March 2023
- Published online by Cambridge University Press:
- 20 January 2022, pp. 794-826
- Print publication:
- March 2023
-
- Article
- Export citation
FIXED POINT THEOREM FOR AN INFINITE TOEPLITZ MATRIX
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 104 / Issue 1 / August 2021
- Published online by Cambridge University Press:
- 09 November 2020, pp. 108-117
- Print publication:
- August 2021
-
- Article
- Export citation
On two classes of reflected autoregressive processes
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 57 / Issue 2 / June 2020
- Published online by Cambridge University Press:
- 16 July 2020, pp. 657-678
- Print publication:
- June 2020
-
- Article
- Export citation
RANK GENERATING FUNCTIONS FOR ODD-BALANCED UNIMODAL SEQUENCES, QUANTUM JACOBI FORMS, AND MOCK JACOBI FORMS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 109 / Issue 2 / October 2020
- Published online by Cambridge University Press:
- 10 January 2020, pp. 157-175
- Print publication:
- October 2020
-
- Article
-
- You have access
- Export citation
AN ANALOGUE OF EULER’S IDENTITY AND SPLIT PERFECT PARTITIONS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 99 / Issue 3 / June 2019
- Published online by Cambridge University Press:
- 17 December 2018, pp. 353-361
- Print publication:
- June 2019
-
- Article
-
- You have access
- Export citation