17 results
Hitting times on the lollipop graph
-
- Journal:
- Probability in the Engineering and Informational Sciences , First View
- Published online by Cambridge University Press:
- 07 March 2025, pp. 1-34
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Hitting times for second-order random walks
- Part of
-
- Journal:
- European Journal of Applied Mathematics / Volume 34 / Issue 4 / August 2023
- Published online by Cambridge University Press:
- 04 July 2022, pp. 642-666
-
- Article
- Export citation
LOWER TAIL INDEPENDENCE OF HITTING TIMES OF TWO-DIMENSIONAL DIFFUSIONS
-
- Journal:
- Probability in the Engineering and Informational Sciences / Volume 32 / Issue 4 / October 2018
- Published online by Cambridge University Press:
- 18 September 2017, pp. 522-535
-
- Article
- Export citation
Speed of coming down from infinity for birth-and-death processes
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 48 / Issue 4 / December 2016
- Published online by Cambridge University Press:
- 11 January 2017, pp. 1183-1210
- Print publication:
- December 2016
-
- Article
- Export citation
Path integrals for continuous-time Markov chains
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 39 / Issue 4 / December 2002
- Published online by Cambridge University Press:
- 14 July 2016, pp. 901-904
- Print publication:
- December 2002
-
- Article
- Export citation
A Markovian analysis of additive-increase multiplicative-decrease algorithms
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 34 / Issue 1 / March 2002
- Published online by Cambridge University Press:
- 19 February 2016, pp. 85-111
- Print publication:
- March 2002
-
- Article
- Export citation
On hitting times for compound Poisson dams with exponential jumps and linear release rate
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 38 / Issue 3 / September 2001
- Published online by Cambridge University Press:
- 14 July 2016, pp. 781-786
- Print publication:
- September 2001
-
- Article
- Export citation
Trees with random conductivities and the (reciprocal) inverse Gaussian distribution
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 30 / Issue 2 / June 1998
- Published online by Cambridge University Press:
- 01 July 2016, pp. 409-424
- Print publication:
- June 1998
-
- Article
- Export citation
Stein's method for geometric approximation
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 33 / Issue 3 / September 1996
- Published online by Cambridge University Press:
- 14 July 2016, pp. 707-713
- Print publication:
- September 1996
-
- Article
- Export citation
On crossing times for multidimensional walks with skip-free components
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 32 / Issue 4 / December 1995
- Published online by Cambridge University Press:
- 14 July 2016, pp. 991-1006
- Print publication:
- December 1995
-
- Article
- Export citation
Problèmes de premier passage résolubles par la méthode de séparation des variables
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 32 / Issue 2 / June 1995
- Published online by Cambridge University Press:
- 14 July 2016, pp. 337-348
- Print publication:
- June 1995
-
- Article
- Export citation
Some results involving the maximum of Brownian motion
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 30 / Issue 4 / December 1993
- Published online by Cambridge University Press:
- 14 July 2016, pp. 805-818
- Print publication:
- December 1993
-
- Article
- Export citation
On the dependence structure of hitting times of multivariate processes
-
- Journal:
- Journal of Applied Probability / Volume 26 / Issue 2 / June 1989
- Published online by Cambridge University Press:
- 14 July 2016, pp. 287-295
- Print publication:
- June 1989
-
- Article
- Export citation
Exponential martingales and Wald's formulas for two-queue networks
-
- Journal:
- Journal of Applied Probability / Volume 23 / Issue 3 / September 1986
- Published online by Cambridge University Press:
- 14 July 2016, pp. 812-819
- Print publication:
- September 1986
-
- Article
- Export citation
Criteria for ergodicity, exponential ergodicity and strong ergodicity of Markov processes
-
- Journal:
- Journal of Applied Probability / Volume 18 / Issue 1 / March 1981
- Published online by Cambridge University Press:
- 14 July 2016, pp. 122-130
- Print publication:
- March 1981
-
- Article
- Export citation
Criteria for strong ergodicity of Markov chains
-
- Journal:
- Journal of Applied Probability / Volume 15 / Issue 1 / March 1978
- Published online by Cambridge University Press:
- 14 July 2016, pp. 87-95
- Print publication:
- March 1978
-
- Article
- Export citation
A note on the inverse problem for reducible Markov chains
-
- Journal:
- Journal of Applied Probability / Volume 14 / Issue 3 / September 1977
- Published online by Cambridge University Press:
- 14 July 2016, pp. 621-625
- Print publication:
- September 1977
-
- Article
- Export citation

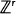 (or
(or 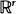 ), one of whose components is skip-free. We obtain identities for distributions of hitting times for the components of the process generalizing the well-known one for the one-dimensional case. These relations reflect the fact that in this case spatial and time coordinates play, in some sense, symmetric roles. They turn out to be useful for solving several problems. For example, they allow us to find the distribution of the number of jumps of the process, which fall in a fixed set before the skip-free component of the process hits a fixed level. Examples are given showing how our results can be applied to models in branching processes, queueing, and risk theory.
), one of whose components is skip-free. We obtain identities for distributions of hitting times for the components of the process generalizing the well-known one for the one-dimensional case. These relations reflect the fact that in this case spatial and time coordinates play, in some sense, symmetric roles. They turn out to be useful for solving several problems. For example, they allow us to find the distribution of the number of jumps of the process, which fall in a fixed set before the skip-free component of the process hits a fixed level. Examples are given showing how our results can be applied to models in branching processes, queueing, and risk theory.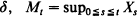 and
and 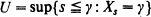 and Δ=
and Δ= 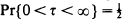 . We also derive various other distributional results involving the pair (
. We also derive various other distributional results involving the pair (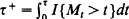 ; in particular we show that, in case
; in particular we show that, in case 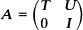 on
on 
