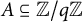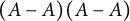7 results
On some multiplicative properties of large difference sets
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 76 / Issue 5 / October 2024
- Published online by Cambridge University Press:
- 08 September 2023, pp. 1538-1555
- Print publication:
- October 2024
-
- Article
-
- You have access
- HTML
- Export citation
11 - Incidences in Rd
-
- Book:
- Polynomial Methods and Incidence Theory
- Published online:
- 17 March 2022
- Print publication:
- 24 March 2022, pp 155-171
-
- Chapter
- Export citation
1 - Incidences and Classical Discrete Geometry
-
- Book:
- Polynomial Methods and Incidence Theory
- Published online:
- 17 March 2022
- Print publication:
- 24 March 2022, pp 1-24
-
- Chapter
- Export citation
8 - Constant-Degree Polynomial Partitioning and Incidences in C2
-
- Book:
- Polynomial Methods and Incidence Theory
- Published online:
- 17 March 2022
- Print publication:
- 24 March 2022, pp 108-124
-
- Chapter
- Export citation
3 - Polynomial Partitioning
-
- Book:
- Polynomial Methods and Incidence Theory
- Published online:
- 17 March 2022
- Print publication:
- 24 March 2022, pp 35-50
-
- Chapter
- Export citation
12 - Incidence Applications in Rd
-
- Book:
- Polynomial Methods and Incidence Theory
- Published online:
- 17 March 2022
- Print publication:
- 24 March 2022, pp 172-181
-
- Chapter
- Export citation

Polynomial Methods and Incidence Theory
-
- Published online:
- 17 March 2022
- Print publication:
- 24 March 2022