Search

We provide examples of infinitesimally Hilbertian, rectifiable, Ahlfors regular metric measure spaces having pmGH-tangents that are not infinitesimally Hilbertian.

The main result of this paper is the following: any weighted Riemannian manifold 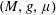$(M,g,\unicode[STIX]{x1D707})$, i.e., a Riemannian manifold 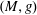$(M,g)$ endowed with a generic non-negative Radon measure 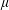$\unicode[STIX]{x1D707}$, is infinitesimally Hilbertian, which means that its associated Sobolev space 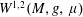$W^{1,2}(M,g,\unicode[STIX]{x1D707})$ is a Hilbert space.

We actually prove a stronger result: the abstract tangent module (à la Gigli) associated with any weighted reversible Finsler manifold 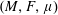$(M,F,\unicode[STIX]{x1D707})$ can be isometrically embedded into the space of all measurable sections of the tangent bundle of 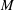$M$ that are 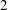$2$-integrable with respect to 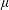$\unicode[STIX]{x1D707}$.