Refine search
Actions for selected content:
31 results
3 - A Review of First Principles
-
- Book:
- Satellite Remote Sensing for Water Management
- Published online:
- 10 October 2025
- Print publication:
- 04 September 2025, pp 42-58
-
- Chapter
- Export citation
Physics-constrained convolutional neural networks for inverse problems in spatiotemporal partial differential equations
-
- Journal:
- Data-Centric Engineering / Volume 5 / 2024
- Published online by Cambridge University Press:
- 20 December 2024, e43
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Honeycomb structure filling morphing wing trailing edge: Design strategy, deformation feedback, and active control
- Part of
-
- Journal:
- Programmable Materials / Volume 2 / 2024
- Published online by Cambridge University Press:
- 03 May 2024, e2
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Characterising small objects in the regime between the eddy current model and wave propagation
- Part of
-
- Journal:
- European Journal of Applied Mathematics / Volume 35 / Issue 2 / April 2024
- Published online by Cambridge University Press:
- 08 August 2023, pp. 294-317
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Chapter 7 - Inference in Perception
-
- Book:
- Problem Solving
- Published online:
- 23 June 2022
- Print publication:
- 07 July 2022, pp 111-127
-
- Chapter
- Export citation
Bayesian optimization with informative parametric models via sequential Monte Carlo
-
- Journal:
- Data-Centric Engineering / Volume 3 / 2022
- Published online by Cambridge University Press:
- 08 March 2022, e5
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
RECOVERY OF ZEROTH ORDER COEFFICIENTS IN NON-LINEAR WAVE EQUATIONS
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 21 / Issue 2 / March 2022
- Published online by Cambridge University Press:
- 18 September 2020, pp. 367-393
- Print publication:
- March 2022
-
- Article
- Export citation
Learning and meta-learning of stochastic advection–diffusion–reaction systems from sparse measurements
- Part of
-
- Journal:
- European Journal of Applied Mathematics / Volume 32 / Issue 3 / June 2021
- Published online by Cambridge University Press:
- 15 June 2020, pp. 397-420
-
- Article
- Export citation
Alternating direction method of multiplier for solving electromagnetic inverse scattering problems
-
- Journal:
- International Journal of Microwave and Wireless Technologies / Volume 12 / Issue 8 / October 2020
- Published online by Cambridge University Press:
- 11 March 2020, pp. 790-796
-
- Article
- Export citation
RECOVERY OF NON-COMPACTLY SUPPORTED COEFFICIENTS OF ELLIPTIC EQUATIONS ON AN INFINITE WAVEGUIDE
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 19 / Issue 5 / September 2020
- Published online by Cambridge University Press:
- 05 November 2018, pp. 1573-1600
- Print publication:
- September 2020
-
- Article
- Export citation
Numerical determination of anomalies in multifrequency electrical impedance tomography
-
- Journal:
- European Journal of Applied Mathematics / Volume 30 / Issue 3 / June 2019
- Published online by Cambridge University Press:
- 17 May 2018, pp. 481-504
-
- Article
- Export citation
A global stability estimate for the photo-acoustic inverse problem in layered media
- Part of
-
- Journal:
- European Journal of Applied Mathematics / Volume 30 / Issue 3 / June 2019
- Published online by Cambridge University Press:
- 17 May 2018, pp. 505-528
-
- Article
- Export citation
Uniqueness in the determination of loads in multi-span beams and plates
-
- Journal:
- European Journal of Applied Mathematics / Volume 30 / Issue 1 / February 2019
- Published online by Cambridge University Press:
- 10 January 2018, pp. 176-195
-
- Article
- Export citation
Size estimates of unknown boundaries with a Robin-type condition
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 147 / Issue 4 / August 2017
- Published online by Cambridge University Press:
- 16 March 2017, pp. 727-741
- Print publication:
- August 2017
-
- Article
- Export citation
Borg's Periodicity Theorems for First-Order Self-Adjoint Systems with Complex Potentials
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 60 / Issue 3 / August 2017
- Published online by Cambridge University Press:
- 19 December 2016, pp. 615-633
-
- Article
- Export citation
Identification of Elastic Orthotropic Material Parameters by the Singular Boundary Method
- Part of
-
- Journal:
- Advances in Applied Mathematics and Mechanics / Volume 8 / Issue 5 / October 2016
- Published online by Cambridge University Press:
- 08 July 2016, pp. 810-826
- Print publication:
- October 2016
-
- Article
- Export citation
A Multilevel Method for the Solution of Time Dependent Optimal Transport
-
- Journal:
- Numerical Mathematics: Theory, Methods and Applications / Volume 8 / Issue 1 / February 2015
- Published online by Cambridge University Press:
- 03 March 2015, pp. 97-111
- Print publication:
- February 2015
-
- Article
- Export citation
Numerical Analysis of an Adaptive FEM for Distributed Flux Reconstruction
-
- Journal:
- Communications in Computational Physics / Volume 15 / Issue 4 / April 2014
- Published online by Cambridge University Press:
- 03 June 2015, pp. 1068-1090
- Print publication:
- April 2014
-
- Article
- Export citation
Reconstruction of Structured Quadratic Pencils from Eigenvalueson Ellipses and Parabolas
-
- Journal:
- Mathematical Modelling of Natural Phenomena / Volume 9 / Issue 5 / 2014
- Published online by Cambridge University Press:
- 17 July 2014, pp. 138-147
- Print publication:
- 2014
-
- Article
- Export citation
Adaptive hard-thresholding for linear inverse problems
-
- Journal:
- ESAIM: Probability and Statistics / Volume 17 / 2013
- Published online by Cambridge University Press:
- 03 June 2013, pp. 485-499
- Print publication:
- 2013
-
- Article
- Export citation

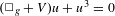
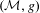

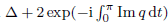 are double zeros if and only if this self-adjoint system is unitarily equivalent to one in which
are double zeros if and only if this self-adjoint system is unitarily equivalent to one in which 