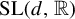Refine search
Actions for selected content:
5 results
Poissonian pair correlation for directions in multi-dimensional affine lattices and escape of mass estimates for embedded horospheres
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 45 / Issue 1 / January 2025
- Published online by Cambridge University Press:
- 26 April 2024, pp. 218-246
- Print publication:
- January 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
On the distribution of the digits of quotients of integers and primes
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 65 / Issue 2 / June 2022
- Published online by Cambridge University Press:
- 11 May 2021, pp. 279-295
- Print publication:
- June 2022
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Critical Dimensions for counting Lattice Points in EuclideanAnnuli
-
- Journal:
- Mathematical Modelling of Natural Phenomena / Volume 5 / Issue 4 / 2010
- Published online by Cambridge University Press:
- 12 May 2010, pp. 293-316
- Print publication:
- 2010
-
- Article
- Export citation
The asymptotic behaviour of the mean-square of fractional part sums
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 43 / Issue 2 / June 2000
- Published online by Cambridge University Press:
- 20 January 2009, pp. 309-323
-
- Article
-
- You have access
- Export citation
Exponential Sums and Lattice Points III
-
- Journal:
- Proceedings of the London Mathematical Society / Volume 87 / Issue 3 / November 2003
- Published online by Cambridge University Press:
- 23 October 2003, pp. 591-609
- Print publication:
- November 2003
-
- Article
- Export citation