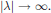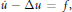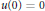Refine search
Actions for selected content:
8 results
The invariant subspaces of periodic Fourier multipliers with application to abstract evolution equations
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 24 June 2025, pp. 1-47
-
- Article
- Export citation
ON THE WELL-POSEDNESS OF PARABOLIC EQUATIONS OF NAVIER–STOKES TYPE WITH
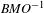 $\mathit{BMO}^{-1}$ DATA
$\mathit{BMO}^{-1}$ DATA
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 16 / Issue 5 / November 2017
- Published online by Cambridge University Press:
- 27 April 2015, pp. 947-985
- Print publication:
- November 2017
-
- Article
- Export citation
An existence result for a system of coupled semilinear diffusion-reaction equations with flux boundary conditions
-
- Journal:
- European Journal of Applied Mathematics / Volume 26 / Issue 2 / April 2015
- Published online by Cambridge University Press:
- 10 December 2014, pp. 121-142
-
- Article
- Export citation
REMARKS ON ℓ1 AND
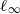 -MAXIMAL REGULARITY FOR POWER-BOUNDED OPERATORS
-MAXIMAL REGULARITY FOR POWER-BOUNDED OPERATORS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 84 / Issue 3 / June 2008
- Published online by Cambridge University Press:
- 01 June 2008, pp. 345-365
- Print publication:
- June 2008
-
- Article
-
- You have access
- Export citation
ON R-SECTORIAL DERIVATIVES ON BERGMAN SPACES
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 77 / Issue 2 / April 2008
- Published online by Cambridge University Press:
- 01 April 2008, pp. 305-313
- Print publication:
- April 2008
-
- Article
-
- You have access
- Export citation
SOLUTIONS OF SECOND-ORDER INTEGRO-DIFFERENTIAL EQUATIONS ON PERIODIC BESOV SPACES
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 50 / Issue 2 / June 2007
- Published online by Cambridge University Press:
- 17 May 2007, pp. 477-492
-
- Article
-
- You have access
- Export citation
The Resolvent of Closed Extensions of Cone Differential Operators
-
- Journal:
- Canadian Journal of Mathematics / Volume 57 / Issue 4 / 01 August 2005
- Published online by Cambridge University Press:
- 20 November 2018, pp. 771-811
- Print publication:
- 01 August 2005
-
- Article
-
- You have access
- Export citation
OPERATOR-VALUED FOURIER MULTIPLIERS ON PERIODIC BESOV SPACES AND APPLICATIONS
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 47 / Issue 1 / February 2004
- Published online by Cambridge University Press:
- 27 May 2004, pp. 15-33
-
- Article
-
- You have access
- Export citation
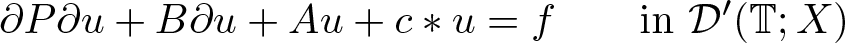
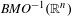
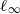 -MAXIMAL REGULARITY FOR POWER-BOUNDED OPERATORS
-MAXIMAL REGULARITY FOR POWER-BOUNDED OPERATORS
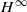 -calculus, and give a complete characterization of this condition in the case of Banach spaces which are
-calculus, and give a complete characterization of this condition in the case of Banach spaces which are