2 - ACC for Log Canonical Thresholds for Complex Analytic Spaces
-
- Book:
- Higher Dimensional Algebraic Geometry
- Published online:
- 06 December 2024
- Print publication:
- 02 January 2025, pp 11-18
-
- Chapter
- Export citation
A REMARK ON FUJINO’S WORK ON THE CANONICAL BUNDLE FORMULA VIA PERIOD MAPS
- Part of
-
- Journal:
- Nagoya Mathematical Journal , First View
- Published online by Cambridge University Press:
- 02 December 2024, pp. 1-14
-
- Article
- Export citation
1 - The Minimal Model Program
-
- Book:
- Complex Algebraic Threefolds
- Published online:
- 29 September 2023
- Print publication:
- 19 October 2023, pp 1-58
-
- Chapter
- Export citation

Complex Algebraic Threefolds
-
- Published online:
- 29 September 2023
- Print publication:
- 19 October 2023
Shokurov’s conjecture on conic bundles with canonical singularities
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 10 / 2022
- Published online by Cambridge University Press:
- 09 June 2022, e38
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
BIRATIONAL RIGIDITY OF ORBIFOLD DEGREE 2 DEL PEZZO FIBRATIONS
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 248 / December 2022
- Published online by Cambridge University Press:
- 02 June 2022, pp. 888-921
- Print publication:
- December 2022
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Geometric consistency of Manin's conjecture
- Part of
-
- Journal:
- Compositio Mathematica / Volume 158 / Issue 6 / June 2022
- Published online by Cambridge University Press:
- 22 August 2022, pp. 1375-1427
- Print publication:
- June 2022
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
ON THE FIRST STEPS OF THE MINIMAL MODEL PROGRAM FOR THE MODULI SPACE OF STABLE POINTED CURVES
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 22 / Issue 1 / January 2023
- Published online by Cambridge University Press:
- 22 April 2021, pp. 145-211
- Print publication:
- January 2023
-
- Article
-
- You have access
- Open access
- Export citation
ON DEL PEZZO FIBRATIONS IN POSITIVE CHARACTERISTIC
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 21 / Issue 1 / January 2022
- Published online by Cambridge University Press:
- 30 March 2020, pp. 197-239
- Print publication:
- January 2022
-
- Article
- Export citation
Higher-dimensional foliated Mori theory
- Part of
-
- Journal:
- Compositio Mathematica / Volume 156 / Issue 1 / January 2020
- Published online by Cambridge University Press:
- 14 November 2019, pp. 1-38
- Print publication:
- January 2020
-
- Article
- Export citation
The non-archimedean SYZ fibration
- Part of
-
- Journal:
- Compositio Mathematica / Volume 155 / Issue 5 / May 2019
- Published online by Cambridge University Press:
- 30 April 2019, pp. 953-972
- Print publication:
- May 2019
-
- Article
- Export citation
Mori's Program for
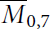 with Symmetric Divisors
with Symmetric Divisors
-
- Journal:
- Canadian Journal of Mathematics / Volume 69 / Issue 3 / 01 June 2017
- Published online by Cambridge University Press:
- 20 November 2018, pp. 613-649
- Print publication:
- 01 June 2017
-
- Article
-
- You have access
- Export citation
The isotriviality of smooth families of canonically polarized manifolds over a special quasi-projective base
- Part of
-
- Journal:
- Compositio Mathematica / Volume 152 / Issue 7 / July 2016
- Published online by Cambridge University Press:
- 26 April 2016, pp. 1421-1434
- Print publication:
- July 2016
-
- Article
- Export citation
Jordan property for groups of birational selfmaps
- Part of
-
- Journal:
- Compositio Mathematica / Volume 150 / Issue 12 / December 2014
- Published online by Cambridge University Press:
- 17 September 2014, pp. 2054-2072
- Print publication:
- December 2014
-
- Article
- Export citation
Stability conditions and birational geometry of projective surfaces
- Part of
-
- Journal:
- Compositio Mathematica / Volume 150 / Issue 10 / October 2014
- Published online by Cambridge University Press:
- 17 July 2014, pp. 1755-1788
- Print publication:
- October 2014
-
- Article
- Export citation
Log pluricanonical representations and the abundance conjecture
- Part of
-
- Journal:
- Compositio Mathematica / Volume 150 / Issue 4 / April 2014
- Published online by Cambridge University Press:
- 10 March 2014, pp. 593-620
- Print publication:
- April 2014
-
- Article
- Export citation
On the Log Canonical Inversion of Adjunction
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 57 / Issue 1 / February 2014
- Published online by Cambridge University Press:
- 19 December 2013, pp. 139-143
-
- Article
-
- You have access
- Export citation
Relations in the Sarkisov program
- Part of
-
- Journal:
- Compositio Mathematica / Volume 149 / Issue 10 / October 2013
- Published online by Cambridge University Press:
- 28 August 2013, pp. 1685-1709
- Print publication:
- October 2013
-
- Article
- Export citation
Families of canonically polarized manifolds over log Fano varieties
- Part of
-
- Journal:
- Compositio Mathematica / Volume 149 / Issue 6 / June 2013
- Published online by Cambridge University Press:
- 26 March 2013, pp. 1019-1040
- Print publication:
- June 2013
-
- Article
- Export citation
Modular compactifications of the space of pointed elliptic curves II
- Part of
-
- Journal:
- Compositio Mathematica / Volume 147 / Issue 6 / November 2011
- Published online by Cambridge University Press:
- 30 August 2011, pp. 1843-1884
- Print publication:
- November 2011
-
- Article
-
- You have access
- Export citation

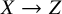
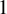
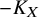
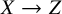

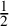
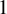
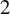
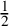
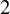
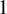
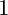
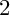
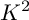
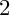
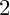
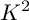
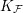
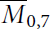 with Symmetric Divisors
with Symmetric Divisors
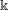
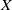
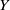
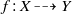
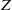
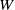
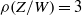
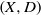
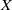
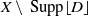
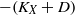
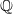
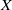
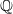
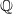
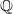
 .
.
