1 results
Topological full groups of minimal subshifts and quantifying local embeddings into finite groups
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 43 / Issue 5 / May 2023
- Published online by Cambridge University Press:
- 05 April 2022, pp. 1492-1510
- Print publication:
- May 2023
-
- Article
-
- You have access
- HTML
- Export citation
-
We investigate quantitative aspects of the locally embeddable into finite groups (LEF) property for subgroups of the topological full group
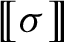of a two-sided minimal subshift over a finite alphabet, measured via the LEF growth function. We show that the LEF growth of
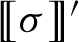may be bounded from above and below in terms of the recurrence function and the complexity function of the subshift, respectively. As an application, we construct groups of previously unseen LEF growth types, and exhibit a continuum of finitely generated LEF groups which may be distinguished from one another by their LEF growth.
