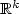In this paper we are interested in the estimation of a density − defined on a compact interval ofℝ− from n independent andidentically distributed observations. In order to avoid boundary effect, beta kernelestimators are used and we propose a procedure (inspired by Lepski’s method) in order toselect the bandwidth. Our procedure is proved to be adaptive in an asymptotically minimaxframework. Our estimator is compared with both the cross-validation algorithm and theoracle estimator using simulated data.

We consider the problem of estimating an unknown regression function when the design is random with values in $\mathbb{R}^k$. Our estimation procedure is based on model selection and does not rely on any prior information on the target function. We start with a collection of linear functional spaces and build, on a data selected space among this collection, the least-squares estimator. We study the performance of an estimator which is obtained by modifying this least-squares estimator on a set of small probability. For the so-defined estimator, we establish nonasymptotic risk bounds that can be related to oracle inequalities. As a consequence of these, we show that our estimator possesses adaptive properties in the minimax sense over large families of Besov balls Bα,l,∞(R) with R>0, l ≥ 1 and α > α1 where α1 is a positive number satisfying 1/l - 1/2 ≤ α1 < 1/l. We also study the particular case where the regression function is additive and then obtain an additive estimator which converges at the same rate as it does when k=1.