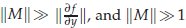This paper is devoted to an extension of the finite-energy condition for extended Runge-Kutta-Nyström (ERKN) integrators and applications to nonlinear wave equations. We begin with an error analysis for the integrators for multi-frequency highly oscillatory systems , where M is positive semi-definite, . The highly oscillatory system is due to the semi-discretisation of conservative, or dissipative, nonlinear wave equations. The structure of such a matrix 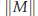M and initial conditions are based on particular spatial discretisations. Similarly to the error analysis for Gaustchi-type methods of order two, where a finite-energy condition bounding amplitudes of high oscillations is satisfied by the solution, a finite-energy condition for the semi-discretisation of nonlinear wave equations is introduced and analysed. These ensure that the error bound of ERKN methods is independent of . Since stepsizes are not restricted by frequencies of M, large stepsizes can be employed by our ERKN integrators of arbitrary high order. Numerical experiments provided in this paper have demonstrated that our results are truly promising, and consistent with our analysis and prediction.