One of the most fundamental properties of a proof system is analyticity, expressing the fact that a proof of a given formula F only uses subformulas of F. In sequent calculus, this property is usually proved by showing that the
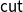 $\mathsf{cut}$
rule is admissible, i.e., the introduction of the auxiliary lemma H in the reasoning “if H follows from G and F follows from H, then F follows from G” can be eliminated. The proof of cut admissibility is usually a tedious, error-prone process through several proof transformations, thus requiring the assistance of (semi-)automatic procedures. In a previous work by Miller and Pimentel, linear logic (
$\mathsf{cut}$
rule is admissible, i.e., the introduction of the auxiliary lemma H in the reasoning “if H follows from G and F follows from H, then F follows from G” can be eliminated. The proof of cut admissibility is usually a tedious, error-prone process through several proof transformations, thus requiring the assistance of (semi-)automatic procedures. In a previous work by Miller and Pimentel, linear logic (
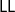 $\mathsf{LL}$
) was used as a logical framework for establishing sufficient conditions for cut admissibility of object logical systems (OL). The OL’s inference rules are specified as an
$\mathsf{LL}$
) was used as a logical framework for establishing sufficient conditions for cut admissibility of object logical systems (OL). The OL’s inference rules are specified as an
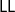 $\mathsf{LL}$
theory and an easy-to-verify criterion sufficed to establish the cut-admissibility theorem for the OL at hand. However, there are many logical systems that cannot be adequately encoded in
$\mathsf{LL}$
theory and an easy-to-verify criterion sufficed to establish the cut-admissibility theorem for the OL at hand. However, there are many logical systems that cannot be adequately encoded in
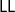 $\mathsf{LL}$
, the most symptomatic cases being sequent systems for modal logics. In this paper, we use a linear-nested sequent (
$\mathsf{LL}$
, the most symptomatic cases being sequent systems for modal logics. In this paper, we use a linear-nested sequent (
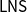 $\mathsf{LNS}$
) presentation of
$\mathsf{LNS}$
) presentation of
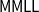 $\mathsf{MMLL}$
(a variant of LL with subexponentials), and show that it is possible to establish a cut-admissibility criterion for
$\mathsf{MMLL}$
(a variant of LL with subexponentials), and show that it is possible to establish a cut-admissibility criterion for
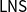 $\mathsf{LNS}$
systems for (classical or substructural) multimodal logics. We show that the same approach is suitable for handling the
$\mathsf{LNS}$
systems for (classical or substructural) multimodal logics. We show that the same approach is suitable for handling the
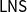 $\mathsf{LNS}$
system for intuitionistic logic.
$\mathsf{LNS}$
system for intuitionistic logic.