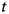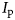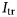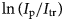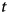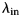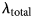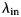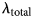7 results
7 - Theoretical Fundamentals of Micro/Nanoscale Thermal Radiation
-
- Book:
- Thermal Radiation
- Published online:
- 31 October 2024
- Print publication:
- 14 November 2024, pp 137-236
-
- Chapter
- Export citation
High-Energy Electron Scattering in Thick Samples Evaluated by Bright-Field Transmission Electron Microscopy, Energy-Filtering Transmission Electron Microscopy, and Electron Tomography
-
- Journal:
- / Volume 28 / Issue 3 / June 2022
- Published online by Cambridge University Press:
- 28 March 2022, pp. 659-671
- Print publication:
- June 2022
-
- Article
- Export citation
7 - Polarized Target Materials
-
- Book:
- The Physics of Polarized Targets
- Published online:
- 03 February 2020
- Print publication:
- 16 January 2020, pp 283-338
-
- Chapter
- Export citation
The Influence of Beam Broadening on the Spatial Resolution of Annular Dark Field Scanning Transmission Electron Microscopy
-
- Journal:
- / Volume 24 / Issue 1 / February 2018
- Published online by Cambridge University Press:
- 27 February 2018, pp. 8-16
- Print publication:
- February 2018
-
- Article
-
- You have access
- HTML
- Export citation
Highly Automated Electron Energy-Loss Spectroscopy Elemental Quantification
-
- Journal:
- / Volume 20 / Issue 3 / June 2014
- Published online by Cambridge University Press:
- 10 April 2014, pp. 798-806
- Print publication:
- June 2014
-
- Article
- Export citation
Effect of Interface Anisotropy on Elastic Wave Propagation in Particulate Composites
-
- Journal:
- Journal of Mechanics / Volume 24 / Issue 1 / March 2008
- Published online by Cambridge University Press:
- 05 May 2011, pp. 79-93
- Print publication:
- March 2008
-
- Article
- Export citation
Shock-tube experiments on Richtmyer–Meshkov instability growth using an enlarged double-bump perturbation
-
- Journal:
- Laser and Particle Beams / Volume 21 / Issue 3 / July 2003
- Published online by Cambridge University Press:
- 03 March 2004, pp. 411-418
-
- Article
- Export citation