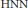14 results
ON MALLE’S CONJECTURE FOR THE PRODUCT OF SYMMETRIC AND NILPOTENT GROUPS
- Part of
-
- Journal:
- Nagoya Mathematical Journal , First View
- Published online by Cambridge University Press:
- 17 February 2025, pp. 1-26
-
- Article
- Export citation
ALMOST ABELIAN NUMBERS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society , First View
- Published online by Cambridge University Press:
- 20 December 2024, pp. 1-6
-
- Article
-
- You have access
- HTML
- Export citation
On the critical regularity of nilpotent groups acting on the interval: the metabelian case
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 45 / Issue 4 / April 2025
- Published online by Cambridge University Press:
- 24 September 2024, pp. 1177-1198
- Print publication:
- April 2025
-
- Article
-
- You have access
- HTML
- Export citation
Conjugacy growth in the higher Heisenberg groups
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 65 / Issue S1 / May 2023
- Published online by Cambridge University Press:
- 23 January 2023, pp. S148-S169
- Print publication:
- May 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Nilpotent n-tuples in SU(2)
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 63 / Issue 4 / November 2020
- Published online by Cambridge University Press:
- 30 September 2020, pp. 1005-1030
-
- Article
- Export citation
PROPERTIES OF FINITE GROUPS DETERMINED BY THE PRODUCT OF THEIR ELEMENT ORDERS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 103 / Issue 1 / February 2021
- Published online by Cambridge University Press:
- 01 June 2020, pp. 88-95
- Print publication:
- February 2021
-
- Article
- Export citation
SMALL DOUBLING IN ORDERED GROUPS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 96 / Issue 3 / June 2014
- Published online by Cambridge University Press:
- 30 April 2014, pp. 316-325
- Print publication:
- June 2014
-
- Article
-
- You have access
- Export citation
Camina Triples
-
- Journal:
- Canadian Mathematical Bulletin / Volume 57 / Issue 1 / 14 March 2014
- Published online by Cambridge University Press:
- 20 November 2018, pp. 125-131
- Print publication:
- 14 March 2014
-
- Article
-
- You have access
- Export citation
FINITELY GENERATED SOLUBLE GROUPS WITH A CONDITION ON INFINITE SUBSETS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 87 / Issue 1 / February 2013
- Published online by Cambridge University Press:
- 13 June 2012, pp. 152-157
- Print publication:
- February 2013
-
- Article
-
- You have access
- Export citation
COHOMOLOGY AND PROFINITE TOPOLOGIES FOR SOLVABLE GROUPS OF FINITE RANK
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 86 / Issue 2 / October 2012
- Published online by Cambridge University Press:
- 16 February 2012, pp. 254-265
- Print publication:
- October 2012
-
- Article
-
- You have access
- Export citation
Isometric Group Actions on Hilbert Spaces: Structure of Orbits
-
- Journal:
- Canadian Journal of Mathematics / Volume 60 / Issue 5 / October 2008
- Published online by Cambridge University Press:
- 20 November 2018, pp. 1001-1009
- Print publication:
- October 2008
-
- Article
-
- You have access
- Export citation
A COUNTEREXAMPLE TO METRIC DIFFERENTIABILITY
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 46 / Issue 1 / February 2003
- Published online by Cambridge University Press:
- 27 January 2003, pp. 221-227
-
- Article
-
- You have access
- Export citation
Cyclic Subgroup Separability of HNN-Extensions with Cyclic Associated Subgroups
-
- Journal:
- Canadian Mathematical Bulletin / Volume 42 / Issue 3 / 01 September 1999
- Published online by Cambridge University Press:
- 20 November 2018, pp. 335-343
- Print publication:
- 01 September 1999
-
- Article
-
- You have access
- Export citation
On the Residual Finiteness of Polygonal Products of Nilpotent Groups
-
- Journal:
- Canadian Mathematical Bulletin / Volume 35 / Issue 3 / 01 September 1992
- Published online by Cambridge University Press:
- 20 November 2018, pp. 390-399
- Print publication:
- 01 September 1992
-
- Article
-
- You have access
- Export citation

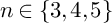
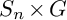
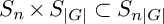
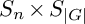
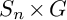


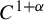


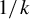

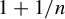
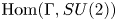
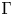
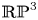
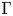
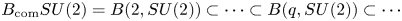
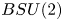
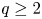
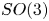
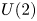
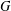
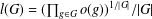
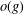
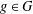
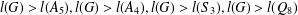
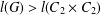
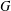
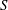
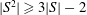
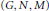
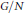
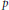
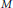
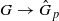 induces an isomorphism
induces an isomorphism 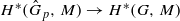 for any discrete
for any discrete 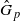 -module
-module 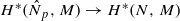 is an isomorphism for any discrete
is an isomorphism for any discrete 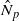 -module
-module