Let G be a locally compact unimodular group, and let 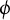 $\phi $ be some function of n variables on G. To such a
$\phi $ be some function of n variables on G. To such a 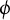 $\phi $, one can associate a multilinear Fourier multiplier, which acts on some n-fold product of the noncommutative
$\phi $, one can associate a multilinear Fourier multiplier, which acts on some n-fold product of the noncommutative 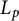 $L_p$-spaces of the group von Neumann algebra. One may also define an associated Schur multiplier, which acts on an n-fold product of Schatten classes
$L_p$-spaces of the group von Neumann algebra. One may also define an associated Schur multiplier, which acts on an n-fold product of Schatten classes 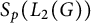 $S_p(L_2(G))$. We generalize well-known transference results from the linear case to the multilinear case. In particular, we show that the so-called “multiplicatively bounded
$S_p(L_2(G))$. We generalize well-known transference results from the linear case to the multilinear case. In particular, we show that the so-called “multiplicatively bounded  $(p_1,\ldots ,p_n)$-norm” of a multilinear Schur multiplier is bounded above by the corresponding multiplicatively bounded norm of the Fourier multiplier, with equality whenever the group is amenable. Furthermore, we prove that the bilinear Hilbert transform is not bounded as a vector-valued map
$(p_1,\ldots ,p_n)$-norm” of a multilinear Schur multiplier is bounded above by the corresponding multiplicatively bounded norm of the Fourier multiplier, with equality whenever the group is amenable. Furthermore, we prove that the bilinear Hilbert transform is not bounded as a vector-valued map 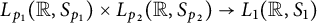 $L_{p_1}(\mathbb {R}, S_{p_1}) \times L_{p_2}(\mathbb {R}, S_{p_2}) \rightarrow L_{1}(\mathbb {R}, S_{1})$, whenever
$L_{p_1}(\mathbb {R}, S_{p_1}) \times L_{p_2}(\mathbb {R}, S_{p_2}) \rightarrow L_{1}(\mathbb {R}, S_{1})$, whenever 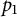 $p_1$ and
$p_1$ and 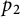 $p_2$ are such that
$p_2$ are such that 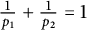 $\frac {1}{p_1} + \frac {1}{p_2} = 1$. A similar result holds for certain Calderón–Zygmund-type operators. This is in contrast to the nonvector-valued Euclidean case.
$\frac {1}{p_1} + \frac {1}{p_2} = 1$. A similar result holds for certain Calderón–Zygmund-type operators. This is in contrast to the nonvector-valued Euclidean case.
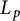 $L_p$-spaces
$L_p$-spaces