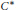1 results
A Representation Theorem for Archimedean Quadratic Modules on ∗-Rings
-
- Journal:
- Canadian Mathematical Bulletin / Volume 52 / Issue 1 / 01 March 2009
- Published online by Cambridge University Press:
- 20 November 2018, pp. 39-52
- Print publication:
- 01 March 2009
-
- Article
-
- You have access
- Export citation
-
We present a new approach to noncommutative real algebraic geometry based on the representation theory of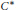
${{C}^{*}}$-algebras. An important result in commutative real algebraic geometry is Jacobi's representation theorem for archimedean quadratic modules on commutative rings. We show that this theorem is a consequence of the Gelfand–Naimark representation theorem for commutative
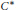${{C}^{*}}$-algebras. A noncommutative version of Gelfand–Naimark theory was studied by I. Fujimoto. We use his results to generalize Jacobi's theorem to associative rings with involution.
