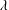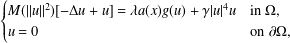Refine search
Actions for selected content:
4 results
Fractional eigenvalue problems that approximate Steklov eigenvalue problems
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 148 / Issue 3 / June 2018
- Published online by Cambridge University Press:
- 28 December 2017, pp. 499-516
- Print publication:
- June 2018
-
- Article
- Export citation
EXISTENCE OF POSITIVE SOLUTION FOR INDEFINITE KIRCHHOFF EQUATION IN EXTERIOR DOMAINS WITH SUBCRITICAL OR CRITICAL GROWTH
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 103 / Issue 3 / December 2017
- Published online by Cambridge University Press:
- 23 December 2016, pp. 329-340
- Print publication:
- December 2017
-
- Article
-
- You have access
- Export citation
The polarization in a ferroelectric thin film: local andnonlocal limit problems
-
- Journal:
- ESAIM: Control, Optimisation and Calculus of Variations / Volume 19 / Issue 3 / July 2013
- Published online by Cambridge University Press:
- 28 March 2013, pp. 657-667
- Print publication:
- July 2013
-
- Article
- Export citation
Numerical Approximations of the Relative Rearrangement:The piecewise linear case.Application to some Nonlocal Problems
-
- Journal:
- ESAIM: Mathematical Modelling and Numerical Analysis / Volume 34 / Issue 2 / March 2000
- Published online by Cambridge University Press:
- 15 April 2002, pp. 477-499
- Print publication:
- March 2000
-
- Article
- Export citation