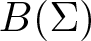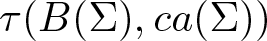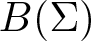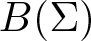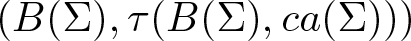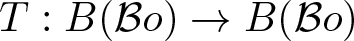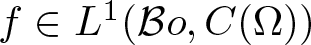Refine search
Actions for selected content:
2 results
On traces of Bochner representable operators on the space of bounded measurable functions
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 67 / Issue 1 / February 2024
- Published online by Cambridge University Press:
- 11 January 2024, pp. 224-235
-
- Article
- Export citation
OPERATORS THAT ARE NUCLEAR WHENEVER THEY ARE NUCLEAR FOR A LARGER RANGE SPACE
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 47 / Issue 3 / October 2004
- Published online by Cambridge University Press:
- 09 November 2004, pp. 679-694
-
- Article
-
- You have access
- Export citation