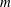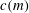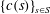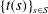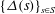3 results
REALISABLE SETS OF CATENARY DEGREES OF NUMERICAL MONOIDS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 97 / Issue 2 / April 2018
- Published online by Cambridge University Press:
- 04 December 2017, pp. 240-245
- Print publication:
- April 2018
-
- Article
-
- You have access
- Export citation
THE CATENARY AND TAME DEGREES ON A NUMERICAL MONOID ARE EVENTUALLY PERIODIC
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 97 / Issue 3 / December 2014
- Published online by Cambridge University Press:
- 09 September 2014, pp. 289-300
- Print publication:
- December 2014
-
- Article
-
- You have access
- Export citation
Elements in a Numerical Semigroup with Factorizations of the Same Length
-
- Journal:
- Canadian Mathematical Bulletin / Volume 54 / Issue 1 / 01 March 2011
- Published online by Cambridge University Press:
- 20 November 2018, pp. 39-43
- Print publication:
- 01 March 2011
-
- Article
-
- You have access
- Export citation