1 results
Linearized stability implies dynamic stability for equilibria of 1-dimensional, p-Laplacian boundary value problems
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 150 / Issue 3 / June 2020
- Published online by Cambridge University Press:
- 29 January 2019, pp. 1313-1338
- Print publication:
- June 2020
-
- Article
- Export citation
-
We consider the parabolic, initial-boundary value problem 1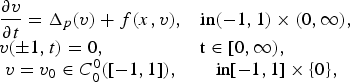
where Δp denotes the p-Laplacian on ( − 1, 1), with p > 1, and the function f:[ − 1, 1] × ℝ → ℝ is continuous, and the partial derivative fv exists and is continuous and bounded on [ − 1, 1] × ℝ. It will be shown that (under certain additional hypotheses) the ‘principle of linearized stability’ holds for equilibrium solutions u0 of (1). That is, the asymptotic stability, or instability, of u0 is determined by the sign of the principal eigenvalue of a suitable linearization of the problem (1) at u0. It is well-known that this principle holds for the semilinear case p = 2 (Δ2 is the linear Laplacian), but has not been shown to hold when p ≠ 2.
$$\matrix{ {\displaystyle{{\partial v} \over {\partial t}} = \Delta _p(v) + f(x,v),} & {{\rm in}({\rm - 1},{\rm 1}) \times ({\rm 0},\infty ),} \cr {v( \pm 1,t) = 0,} \hfill \hfill \hfill & {{\rm t}\in [{\rm 0},\infty ),} \hfill \hfill \cr {v = v_0\in C_0^0 ([-1,1]),} & {{\rm in}[{\rm - 1},{\rm 1}] \times \{ {\rm 0}\} ,} \cr } $$We also consider a bifurcation type problem similar to (1), having a line of trivial solutions. We characterize the stability or instability of the trivial solutions, and the bifurcating, non-trivial solutions, and show that there is an ‘exchange of stability’ at the bifurcation point, analogous to the well-known result when p = 2.
