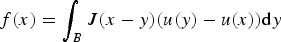3 results
Nonlocal problems in perforated domains
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 150 / Issue 1 / February 2020
- Published online by Cambridge University Press:
- 25 January 2019, pp. 305-340
- Print publication:
- February 2020
-
- Article
- Export citation
Homogenization in perforated domains with rapidly pulsing perforations
-
- Journal:
- ESAIM: Control, Optimisation and Calculus of Variations / Volume 9 / January 2003
- Published online by Cambridge University Press:
- 15 September 2003, pp. 461-483
- Print publication:
- January 2003
-
- Article
- Export citation
Which sequences of holes are admissible for periodic homogenization with Neumann boundary condition?
-
- Journal:
- ESAIM: Control, Optimisation and Calculus of Variations / Volume 8 / 2002
- Published online by Cambridge University Press:
- 15 August 2002, pp. 555-585
- Print publication:
- 2002
-
- Article
- Export citation