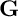3 results
THE DECOMPOSITION OF PERMUTATION MODULE FOR INFINITE CHEVALLEY GROUPS, II
- Part of
-
- Journal:
- Nagoya Mathematical Journal , First View
- Published online by Cambridge University Press:
- 27 December 2024, pp. 1-14
-
- Article
-
- You have access
- HTML
- Export citation
12 - Permutation Actions of M24
-
- Book:
- The Art of Working with the Mathieu Group M24
- Published online:
- 31 October 2024
- Print publication:
- 14 November 2024, pp 165-186
-
- Chapter
- Export citation
ON HIGHER FROBENIUS–SCHUR INDICATORS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 105 / Issue 2 / April 2022
- Published online by Cambridge University Press:
- 12 July 2021, pp. 267-277
- Print publication:
- April 2022
-
- Article
- Export citation