Given partially ordered sets (posets)
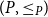 (P, \leq _P\!)
and
(P, \leq _P\!)
and
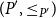 (P^{\prime}, \leq _{P^{\prime}}\!)
, we say that
(P^{\prime}, \leq _{P^{\prime}}\!)
, we say that
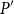 P^{\prime}
contains a copy of
P^{\prime}
contains a copy of
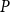 P
if for some injective function
P
if for some injective function
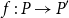 f\,:\, P\rightarrow P^{\prime}
and for any
f\,:\, P\rightarrow P^{\prime}
and for any
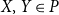 X, Y\in P
,
X, Y\in P
,
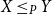 X\leq _P Y
if and only if
X\leq _P Y
if and only if
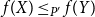 f(X)\leq _{P^{\prime}} f(Y)
. For any posets
f(X)\leq _{P^{\prime}} f(Y)
. For any posets
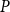 P
and
P
and
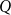 Q
, the poset Ramsey number
Q
, the poset Ramsey number
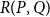 R(P,Q)
is the least positive integer
R(P,Q)
is the least positive integer
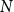 N
such that no matter how the elements of an
N
such that no matter how the elements of an
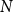 N
-dimensional Boolean lattice are coloured in blue and red, there is either a copy of
N
-dimensional Boolean lattice are coloured in blue and red, there is either a copy of
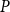 P
with all blue elements or a copy of
P
with all blue elements or a copy of
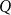 Q
with all red elements. We focus on a poset Ramsey number
Q
with all red elements. We focus on a poset Ramsey number
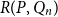 R(P, Q_n)
for a fixed poset
R(P, Q_n)
for a fixed poset
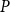 P
and an
P
and an
 n
-dimensional Boolean lattice
n
-dimensional Boolean lattice
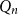 Q_n
, as
Q_n
, as
 n
grows large. We show a sharp jump in behaviour of this number as a function of
n
grows large. We show a sharp jump in behaviour of this number as a function of
 n
depending on whether or not
n
depending on whether or not
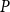 P
contains a copy of either a poset
P
contains a copy of either a poset
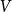 V
, that is a poset on elements
V
, that is a poset on elements
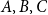 A, B, C
such that
A, B, C
such that
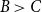 B\gt C
,
B\gt C
,
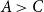 A\gt C
, and
A\gt C
, and
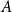 A
and
A
and
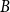 B
incomparable, or a poset
B
incomparable, or a poset
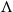 \Lambda
, its symmetric counterpart. Specifically, we prove that if
\Lambda
, its symmetric counterpart. Specifically, we prove that if
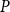 P
contains a copy of
P
contains a copy of
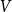 V
or
V
or
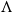 \Lambda
then
\Lambda
then
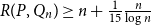 R(P, Q_n) \geq n +\frac{1}{15} \frac{n}{\log n}
. Otherwise
R(P, Q_n) \geq n +\frac{1}{15} \frac{n}{\log n}
. Otherwise
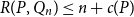 R(P, Q_n) \leq n + c(P)
for a constant
R(P, Q_n) \leq n + c(P)
for a constant
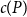 c(P)
. This gives the first non-marginal improvement of a lower bound on poset Ramsey numbers and as a consequence gives
c(P)
. This gives the first non-marginal improvement of a lower bound on poset Ramsey numbers and as a consequence gives
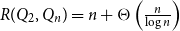 R(Q_2, Q_n) = n + \Theta \left(\frac{n}{\log n}\right)
.
R(Q_2, Q_n) = n + \Theta \left(\frac{n}{\log n}\right)
.