We analyse features of the patterns formed from a simple model for a martensitic phase transition that fragments the unit square into rectangles. This is a fragmentation model that can be encoded by a general branching random walk. An important quantity is the distribution of the lengths of the interfaces in the pattern, and we establish limit theorems for some of the asymptotics of the interface profile. In particular, we are able to use a general branching process to show almost sure power law decay of the number of interfaces of at least a certain size and a general branching random walk to examine the numbers of rectangles of a certain aspect ratio. In doing so we extend a theorem on the growth of the general branching random walk as well as developing results on the tail behaviour of the limiting random variable in our general branching process.

This paper investigates the distributions of triangle counts per vertex and edge, as a means for network description, analysis, model building, and other tasks. The main interest is in estimating these distributions through sampling, especially for large networks. A novel sampling method tailored for the estimation analysis is proposed, with three sampling designs motivated by several network access scenarios. An estimation method based on inversion and an asymptotic method are developed to recover the entire distribution. A single method to estimate the distribution using multiple samples is also considered. Algorithms are presented to sample the network under the various access scenarios. Finally, the estimation methods on synthetic and real-world networks are evaluated in a data study.

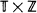For an independent percolation model on , where 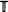is a homogeneous tree and 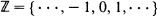is a one-dimensional lattice, it is shown, by verifying that the triangle condition is satisfied, that the percolation probability 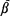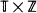θ (p) is a continuous function of p at the critical point pc, and the critical exponents , γ, δ, and Δ exist and take their mean-field values. Some analogous results for Markov fields on are also obtained.