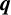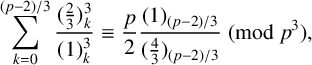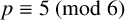We derive a q-supercongruence modulo the third power of a cyclotomic polynomial with the help of Guo and Zudilin’s method of creative microscoping [‘A q-microscope for supercongruences’, Adv. Math. 346 (2019), 329–358] and the q-Dixon formula. As consequences, we give several supercongruences including
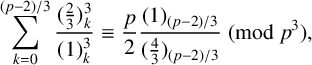 $$ \begin{align*}\sum_{k=0}^{(p-2)/3}\frac{(\frac{2}{3})_k^3}{(1)_k^3}\equiv\frac{p}{2}\frac{(1)_{(p-2)/3}}{(\frac{4}{3})_{(p-2)/3}}\pmod{p^3},\end{align*} $$
$$ \begin{align*}\sum_{k=0}^{(p-2)/3}\frac{(\frac{2}{3})_k^3}{(1)_k^3}\equiv\frac{p}{2}\frac{(1)_{(p-2)/3}}{(\frac{4}{3})_{(p-2)/3}}\pmod{p^3},\end{align*} $$
where p is a prime with
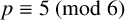 $p\equiv 5\pmod {6}$
.
$p\equiv 5\pmod {6}$
.
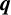 $\boldsymbol {q}$
-SUPERCONGRUENCE MODULO THE THIRD POWER OF A CYCLOTOMIC POLYNOMIAL
$\boldsymbol {q}$
-SUPERCONGRUENCE MODULO THE THIRD POWER OF A CYCLOTOMIC POLYNOMIAL