There are two ways of speeding up Markov chain Monte Carlo algorithms: (a) construct more complex samplers that use gradient and higher-order information about the target and (b) design a control variate to reduce the asymptotic variance. While the efficiency of (a) as a function of dimension has been studied extensively, this paper provides the first results linking the efficiency of (b) with dimension. Specifically, we construct a control variate for a d-dimensional random walk Metropolis chain with an independent, identically distributed target using the solution of the Poisson equation for the scaling limit in [30]. We prove that the asymptotic variance of the corresponding estimator is bounded above by a multiple of 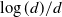$\log(d)/d$ over the spectral gap of the chain. The proof hinges on large deviations theory, optimal Young’s inequality and Berry–Esseen-type bounds. Extensions of the result to non-product targets are discussed.