Refine search
Actions for selected content:
11 results
Zeros of Rankin–Selberg L-functions in families
- Part of
-
- Journal:
- Compositio Mathematica / Volume 160 / Issue 5 / May 2024
- Published online by Cambridge University Press:
- 03 April 2024, pp. 1041-1072
- Print publication:
- May 2024
-
- Article
- Export citation
UNIFORM BOUNDS FOR
 $\operatorname {GL}(3)\times \operatorname {GL}(2)$ L-FUNCTIONS
$\operatorname {GL}(3)\times \operatorname {GL}(2)$ L-FUNCTIONS
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 23 / Issue 4 / July 2024
- Published online by Cambridge University Press:
- 17 October 2023, pp. 1607-1650
- Print publication:
- July 2024
-
- Article
- Export citation
MOMENTS AND HYBRID SUBCONVEXITY FOR SYMMETRIC-SQUARE L-FUNCTIONS
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 22 / Issue 5 / September 2023
- Published online by Cambridge University Press:
- 06 December 2021, pp. 2029-2073
- Print publication:
- September 2023
-
- Article
- Export citation
Sup-norms of eigenfunctions in the level aspect for compact arithmetic surfaces, II: newforms and subconvexity
- Part of
-
- Journal:
- Compositio Mathematica / Volume 156 / Issue 11 / November 2020
- Published online by Cambridge University Press:
- 15 December 2020, pp. 2368-2398
- Print publication:
- November 2020
-
- Article
- Export citation
Motohashi’s fourth moment identity for non-archimedean test functions and applications
- Part of
-
- Journal:
- Compositio Mathematica / Volume 156 / Issue 5 / May 2020
- Published online by Cambridge University Press:
- 17 April 2020, pp. 1004-1038
- Print publication:
- May 2020
-
- Article
- Export citation
Burgess-like subconvexity for
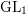 $\text{GL}_{1}$
$\text{GL}_{1}$
- Part of
-
- Journal:
- Compositio Mathematica / Volume 155 / Issue 8 / August 2019
- Published online by Cambridge University Press:
- 04 July 2019, pp. 1457-1499
- Print publication:
- August 2019
-
- Article
- Export citation
EPSTEIN ZETA-FUNCTIONS, SUBCONVEXITY, AND THE PURITY CONJECTURE
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 19 / Issue 2 / March 2020
- Published online by Cambridge University Press:
- 02 April 2018, pp. 581-596
- Print publication:
- March 2020
-
- Article
- Export citation
Sub-Weyl subconvexity for Dirichlet
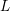 $L$-functions to prime power moduli
$L$-functions to prime power moduli
- Part of
-
- Journal:
- Compositio Mathematica / Volume 152 / Issue 4 / April 2016
- Published online by Cambridge University Press:
- 03 November 2015, pp. 825-875
- Print publication:
- April 2016
-
- Article
- Export citation
Subconvexity and equidistribution of Heegner points in the level aspect
- Part of
-
- Journal:
- Compositio Mathematica / Volume 149 / Issue 7 / July 2013
- Published online by Cambridge University Press:
- 17 June 2013, pp. 1150-1174
- Print publication:
- July 2013
-
- Article
- Export citation
Subconvexity for a double Dirichlet series
- Part of
-
- Journal:
- Compositio Mathematica / Volume 147 / Issue 2 / March 2011
- Published online by Cambridge University Press:
- 07 September 2010, pp. 355-374
- Print publication:
- March 2011
-
- Article
-
- You have access
- Export citation
Subconvexity bounds for automorphic L-functions
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 9 / Issue 1 / January 2010
- Published online by Cambridge University Press:
- 23 July 2009, pp. 95-124
- Print publication:
- January 2010
-
- Article
- Export citation
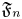
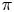
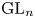
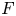
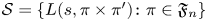
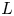
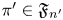
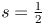
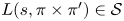
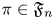
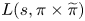
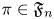

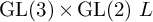
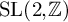
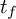
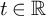
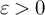
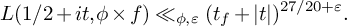
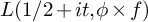
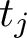
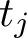
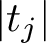
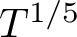
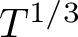
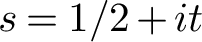
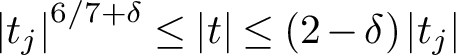
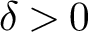
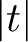
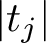
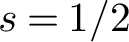
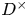
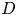
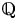
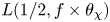
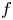
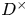
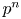
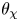
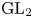
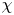
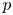
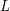
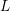
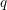
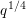
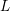
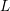
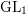
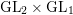
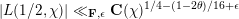
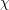
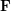
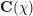
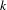
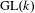
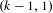
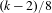
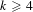
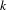
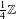
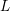
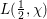
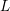
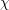
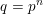
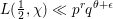

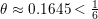
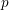
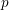
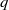
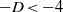
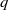
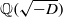
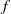
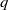
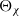
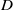
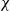
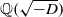
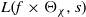
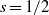
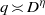
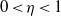
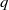
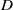
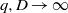
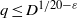
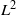
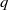
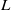
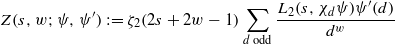
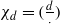 and the subscript 2 denotes the fact that the Euler factor at 2 has been removed. These double Dirichlet series can be extended to
and the subscript 2 denotes the fact that the Euler factor at 2 has been removed. These double Dirichlet series can be extended to 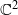 possessing a group of functional equations isomorphic to
possessing a group of functional equations isomorphic to