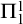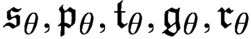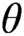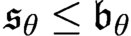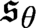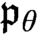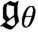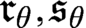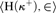We study the consistency and consistency strength of various configurations concerning the cardinal characteristics 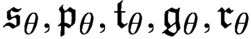 $\mathfrak {s}_\theta , \mathfrak {p}_\theta , \mathfrak {t}_\theta , \mathfrak {g}_\theta , \mathfrak {r}_\theta $
at uncountable regular cardinals
$\mathfrak {s}_\theta , \mathfrak {p}_\theta , \mathfrak {t}_\theta , \mathfrak {g}_\theta , \mathfrak {r}_\theta $
at uncountable regular cardinals 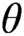 $\theta $
. Motivated by a theorem of Raghavan–Shelah who proved that
$\theta $
. Motivated by a theorem of Raghavan–Shelah who proved that 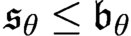 $\mathfrak {s}_\theta \leq \mathfrak {b}_\theta $
, we explore in the first part of the paper the consistency of inequalities comparing
$\mathfrak {s}_\theta \leq \mathfrak {b}_\theta $
, we explore in the first part of the paper the consistency of inequalities comparing 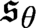 $\mathfrak {s}_\theta $
with
$\mathfrak {s}_\theta $
with 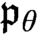 $\mathfrak {p}_\theta $
and
$\mathfrak {p}_\theta $
and 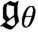 $\mathfrak {g}_\theta $
. In the second part of the paper we study variations of the extender-based Radin forcing to establish several consistency results concerning
$\mathfrak {g}_\theta $
. In the second part of the paper we study variations of the extender-based Radin forcing to establish several consistency results concerning 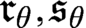 $\mathfrak {r}_\theta ,\mathfrak {s}_\theta $
from hyper-measurability assumptions, results which were previously known to be consistent only from supercompactness assumptions. In doing so, we answer questions from [1], [15] and [7], and improve the large cardinal strength assumptions for results from [10] and [3].
$\mathfrak {r}_\theta ,\mathfrak {s}_\theta $
from hyper-measurability assumptions, results which were previously known to be consistent only from supercompactness assumptions. In doing so, we answer questions from [1], [15] and [7], and improve the large cardinal strength assumptions for results from [10] and [3].