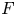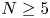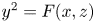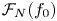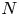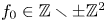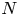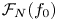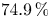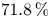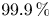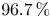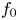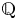Let 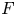F$F$ be a separable integral binary form of odd degree 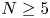N \geq 5$N \geq 5$. A result of Darmon and Granville known as ‘Faltings plus epsilon’ implies that the degree-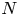N$N$ superelliptic equation 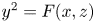y^2 = F(x,z)$y^2 = F(x,z)$ has finitely many primitive integer solutions. In this paper, we consider the family 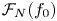\mathscr {F}_N(f_0)$\mathscr {F}_N(f_0)$ of degree-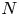N$N$ superelliptic equations with fixed leading coefficient 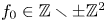f_0 \in \mathbb {Z} \smallsetminus \pm \mathbb {Z}^2$f_0 \in \mathbb {Z} \smallsetminus \pm \mathbb {Z}^2$, ordered by height. For every sufficiently large 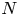N$N$, we prove that among equations in the family 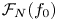\mathscr {F}_N(f_0)$\mathscr {F}_N(f_0)$, more than 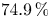74.9\,\%$74.9\,\%$ are insoluble, and more than 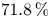71.8\,\%$71.8\,\%$ are everywhere locally soluble but fail the Hasse principle due to the Brauer–Manin obstruction. We further show that these proportions rise to at least 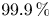99.9\,\%$99.9\,\%$ and 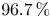96.7\,\%$96.7\,\%$, respectively, when 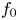f_0$f_0$ has sufficiently many prime divisors of odd multiplicity. Our result can be viewed as a strong asymptotic form of ‘Faltings plus epsilon’ for superelliptic equations and constitutes an analogue of Bhargava's result that most hyperelliptic curves over 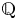\mathbb {Q}$\mathbb {Q}$ have no rational points.