We prove Zhang’s dynamical Manin–Mumford conjecture and dynamical Bogomolov conjecture for dominant endomorphisms
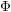 $\unicode[STIX]{x1D6F7}$
of
$\unicode[STIX]{x1D6F7}$
of
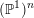 $(\mathbb{P}^{1})^{n}$
. We use the equidistribution theorem for points of small height with respect to an algebraic dynamical system, combined with an analysis of the symmetries of the Julia set for a rational function.
$(\mathbb{P}^{1})^{n}$
. We use the equidistribution theorem for points of small height with respect to an algebraic dynamical system, combined with an analysis of the symmetries of the Julia set for a rational function.
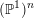 $(\mathbb{P}^{1})^{n}$
$(\mathbb{P}^{1})^{n}$