1 results
On the boundary conditions in estimating ∇ω by div ω and curl ω
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 149 / Issue 3 / June 2019
- Published online by Cambridge University Press:
- 27 December 2018, pp. 739-760
- Print publication:
- June 2019
-
- Article
- Export citation
-
In this paper, we study under what boundary conditions the inequality
holds true. It is known that such an estimate holds if either the tangential or normal component of ω vanishes on the boundary ∂Ω. We show that the vanishing tangential component condition is a special case of a more general one. In two dimensions, we give an interpolation result between these two classical boundary conditions.
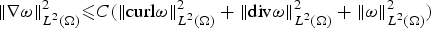$${\rm \Vert }\nabla \omega {\rm \Vert }_{L^2(\Omega )}^2 \les C({\rm \Vert }{\rm curl}\omega {\rm \Vert }_{L^2(\Omega )}^2 + {\rm \Vert }{\rm div}\omega {\rm \Vert }_{L^2(\Omega )}^2 + {\rm \Vert }\omega {\rm \Vert }_{L^2(\Omega )}^2 )$$
