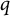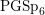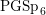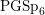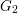6 results
The Kudla–Millson form via the Mathai–Quillen formalism
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 76 / Issue 5 / October 2024
- Published online by Cambridge University Press:
- 05 October 2023, pp. 1638-1663
- Print publication:
- October 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Compatibility of theta lifts and tempered condition
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 67 / Issue 1 / March 2024
- Published online by Cambridge University Press:
- 21 June 2023, pp. 60-73
- Print publication:
- March 2024
-
- Article
-
- You have access
- HTML
- Export citation
Local intertwining relation for metaplectic groups
- Part of
-
- Journal:
- Compositio Mathematica / Volume 156 / Issue 8 / August 2020
- Published online by Cambridge University Press:
- 01 October 2020, pp. 1560-1594
- Print publication:
- August 2020
-
- Article
- Export citation
An exceptional Siegel–Weil formula and poles of the Spin L-function of
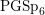 $\text{PGSp}_{6}$
$\text{PGSp}_{6}$
- Part of
-
- Journal:
- Compositio Mathematica / Volume 156 / Issue 6 / June 2020
- Published online by Cambridge University Press:
- 29 May 2020, pp. 1231-1261
- Print publication:
- June 2020
-
- Article
- Export citation
Representations of metaplectic groups I: epsilon dichotomy and local Langlands correspondence
- Part of
-
- Journal:
- Compositio Mathematica / Volume 148 / Issue 6 / November 2012
- Published online by Cambridge University Press:
- 31 October 2012, pp. 1655-1694
- Print publication:
- November 2012
-
- Article
-
- You have access
- Export citation
Endoscopic lifts from PGL3 to G2
-
- Journal:
- Compositio Mathematica / Volume 140 / Issue 3 / May 2004
- Published online by Cambridge University Press:
- 04 December 2007, pp. 793-808
- Print publication:
- May 2004
-
- Article
-
- You have access
- Export citation