We explain and explore class-theoretic potentialism—the view that one can always individuate more classes over a set-theoretic universe. We examine some motivations for class-theoretic potentialism, before proving some results concerning the relevant potentialist systems (in particular exhibiting failures of the $\mathsf {.2}$ and $\mathsf {.3}$ axioms). We then discuss the significance of these results for the different kinds of class-theoretic potentialists.

We introduce a tool for analysing models of $\text {CT}^-$ , the compositional truth theory over Peano Arithmetic. We present a new proof of Lachlan’s theorem that the arithmetical part of models of $\text {CT}^-$ are recursively saturated. We also use this tool to provide a new proof of theorem from [8] that all models of $\text {CT}^-$ carry a partial inductive truth predicate. Finally, we construct a partial truth predicate defined for a set of formulae whose syntactic depth forms a nonstandard cut which cannot be extended to a full truth predicate satisfying $\text {CT}^-$ .

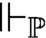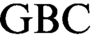The class forcing theorem, which asserts that every class forcing notion ${\mathbb {P}}$ admits a forcing relation $\Vdash _{\mathbb {P}}$ , that is, a relation satisfying the forcing relation recursion—it follows that statements true in the corresponding forcing extensions are forced and forced statements are true—is equivalent over Gödel–Bernays set theory $\text {GBC}$ to the principle of elementary transfinite recursion 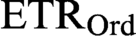$\text {ETR}_{\text {Ord}}$ for class recursions of length 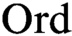$\text {Ord}$ . 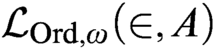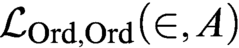It is also equivalent to the existence of truth predicates for the infinitary languages $\mathcal {L}_{\text {Ord},\omega }(\in ,A)$ , allowing any class parameter A; to the existence of truth predicates for the language $\mathcal {L}_{\text {Ord},\text {Ord}}(\in ,A)$ ; to the existence of $\text {Ord}$ -iterated truth predicates for first-order set theory 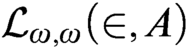$\mathcal {L}_{\omega ,\omega }(\in ,A)$ ; to the assertion that every separative class partial order 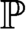${\mathbb {P}}$ has a set-complete class Boolean completion; to a class-join separation principle; and to the principle of determinacy for clopen class games of rank at most 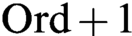$\text {Ord}+1$ . 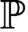Unlike set forcing, if every class forcing notion ${\mathbb {P}}$ has a forcing relation merely for atomic formulas, then every such ${\mathbb {P}}$ has a uniform forcing relation applicable simultaneously to all formulas. Our results situate the class forcing theorem in the rich hierarchy of theories between 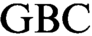$\text {GBC}$ and Kelley–Morse set theory 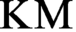$\text {KM}$ .

Let ${\cal T}$ be any of the three canonical truth theories CT− (compositional truth without extra induction), FS− (Friedman–Sheard truth without extra induction), or KF− (Kripke–Feferman truth without extra induction), where the base theory of ${\cal T}$ is PA (Peano arithmetic). We establish the following theorem, which implies that ${\cal T}$ has no more than polynomial speed-up over PA.

Theorem.${\cal T}$is feasibly reducible to PA, in the sense that there is a polynomial time computable function f such that for every${\cal T}$-proof π of an arithmetical sentence ϕ, f (π) is a PA-proof of ϕ.