2 results
‘LIMITING BEHAVIOUR FOR ARRAYS OF UPPER EXTENDED NEGATIVELY DEPENDENT RANDOM VARIABLES’
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 92 / Issue 3 / December 2015
- Published online by Cambridge University Press:
- 06 October 2015, p. 524
- Print publication:
- December 2015
-
- Article
-
- You have access
- Export citation
LIMITING BEHAVIOUR FOR ARRAYS OF UPPER EXTENDED NEGATIVELY DEPENDENT RANDOM VARIABLES
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 92 / Issue 1 / August 2015
- Published online by Cambridge University Press:
- 13 May 2015, pp. 159-167
- Print publication:
- August 2015
-
- Article
-
- You have access
- Export citation
-
For triangular arrays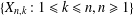
$\{X_{n,k}:1\leqslant k\leqslant n,n\geqslant 1\}$ of upper extended negatively dependent random variables weakly mean dominated by a random variable 
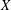$X$ and sequences 
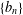$\{b_{n}\}$ of positive constants, conditions are given to guarantee an almost sure finite upper bound to 
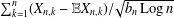$\sum _{k=1}^{n}(X_{n,k}-\mathbb{E}X_{n,k})/\!\sqrt{b_{n}\,\text{Log}\,n}$, where 
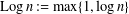$\text{Log}\,n:=\max \{1,\log n\}$, thus getting control over the limiting rate in terms of the prescribed sequence 
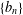$\{b_{n}\}$ and permitting us to weaken or strengthen the assumptions on the random variables.
