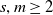1 results
Maximal subgroups of a family of iterated monodromy groups
- Part of
-
- Journal:
- Glasgow Mathematical Journal , First View
- Published online by Cambridge University Press:
- 17 April 2024, pp. 1-22
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
-
The Basilica group is a well-known 2-generated weakly branch, but not branch, group acting on the binary rooted tree. Recently, a more general form of the Basilica group has been investigated by Petschick and Rajeev, which is an
$s$-generated weakly branch, but not branch, group that acts on the 
$m$-adic tree, for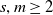 
$s,m\ge 2$. A larger family of groups, which contains these generalised Basilica groups, is the family of iterated monodromy groups. With the new developments by Francoeur, the study of the existence of maximal subgroups of infinite index has been extended from branch groups to weakly branch groups. Here we show that a subfamily of iterated monodromy groups, which more closely resemble the generalised Basilica groups, have maximal subgroups only of finite index.
